دامنهی تابع ${{f}^{-1}}(x)$، برد تابع $f$ است.
چون برد تابع $\mathbb{R}-\left\{ -3 \right\}$ میباشد، پس دامنهی تابع ${{f}^{-1}}(x)$ هم $\mathbb{R}-\left\{ -3 \right\}$ یا $x\ne -3$ است، یعنی گزینهی (2) یا (4).
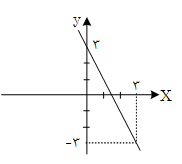
حال ضابطهی $f(x)$ را مییابیم. اگر حفره را فعلا فرض کنیم روی خط باشد:
$\left\{ \begin{matrix} (0,3) \\ (3,-3) \\ \end{matrix}\Rightarrow \right.$ شیب = $m=\frac{3-(-3)}{0-3}=\frac{6}{-3}=-2$
معادلهی خط: $y-3=-2(x-0)\Rightarrow y=-2x+3$
اما چون $x=3$ در دامنهی $f$ وجود ندارد، فرم بهتر معادلهی خط، $x\ne 3$ و $y=-2x+3$ است.
برای محاسبهی ضابطهی تابع وارون، باید $x$ را بر حسب $y$ بیابیم، سپس جای $x$ و $y$ را عوض کنیم:
$y=-2x+3\Rightarrow 2x=3-y\Rightarrow x=\frac{3-y}{2}\xrightarrow{x,y}y={{f}^{-1}}(x)=\frac{3-x}{2},x\ne f(3)\Rightarrow x\ne -3$