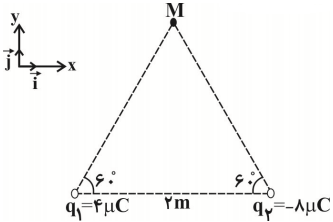
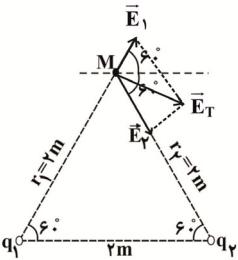
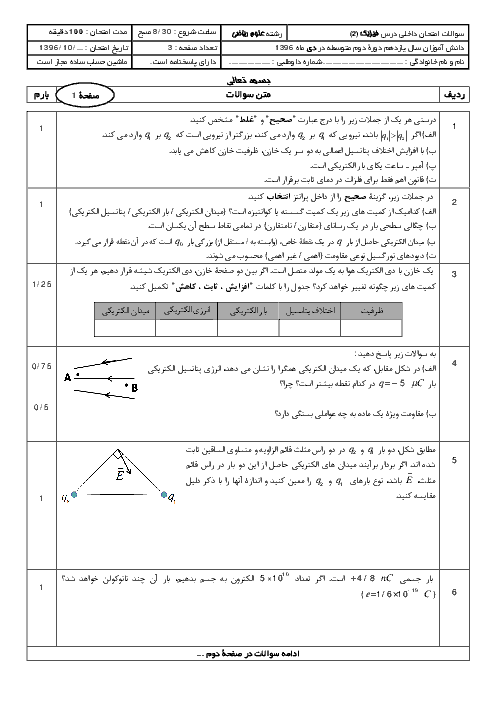
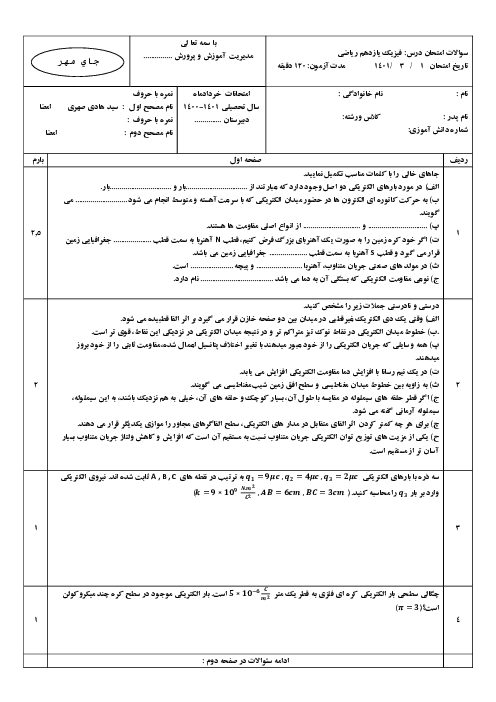
ابتدا اندازهٔ میدان الکتریکی ناشی از بارهای ${{q}_{1}}$ و ${{q}_{2}}$ را در نقطهٔ M می‌یابیم:

${{E}_{1}}\frac{k\left| {{q}_{1}} \right|}{{{r}_{1}}^{2}}=\frac{9\times {{10}^{9}}\times 4\times {{10}^{-6}}}{{{2}^{2}}}=9\times {{10}^{3}}\frac{N}{C}$

${{E}_{2}}=\frac{k\left| {{q}_{2}} \right|}{{{r}_{2}}^{2}}=\frac{9\times {{10}^{9}}\times 8\times {{10}^{-6}}}{{{2}^{2}}}=18\times {{10}^{3}}\frac{N}{C}$

حال میدان‌های $\overrightarrow{{{E}_{1}}}$ و $\overrightarrow{{{E}_{2}}}$ را به‌صورت برداری می‌نویسیم:

$\overrightarrow{{{E}_{1}}}={{E}_{1}}(\cos {{60}^{\circ }}\overrightarrow{i}+\sin {{60}^{\circ }}\overrightarrow{j})=9\times {{10}^{3}}\times (\frac{1}{2}\overrightarrow{i}+\frac{\sqrt{3}}{2}\overrightarrow{j})\frac{N}{C}$

$\overrightarrow{{{E}_{2}}}={{E}_{2}}(\cos {{60}^{\circ }}\overrightarrow{i}-\sin {{60}^{\circ }}\overrightarrow{j})=18\times {{10}^{3}}\times (\frac{1}{2}\overrightarrow{i}-\frac{\sqrt{3}}{2}\overrightarrow{j})\frac{N}{C}$

$\overrightarrow{{{E}_{T}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}=(13/5\overrightarrow{i}-4/5\sqrt{3}\overrightarrow{j})\times {{10}^{3}}\frac{N}{C}$