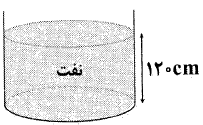
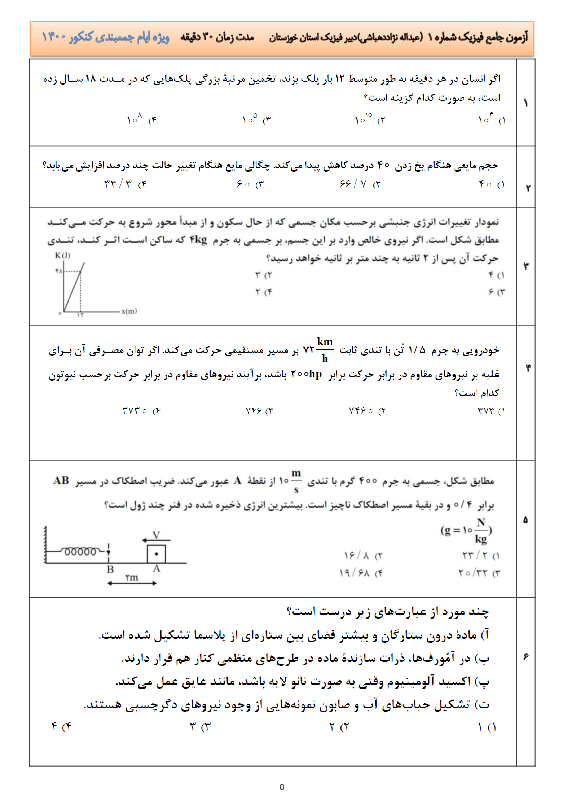
مطابق شکل زیر، ظرف استوانهای شکل را تا ارتفاع $120$ سانتیمتر از نفت به چگالی $0/8\frac{g}{c{{m}^{3}}}$ پر کردهایم و فشار هوای محیط برابر $86/4$ کیلوپاسکال است. برای آنکه فشار کل وارد بر کف ظرف یک درصد کم شود، چن سانتیمتر از ارتفاع نفت را باید کم کنیم؟ ($g=10\frac{m}{{{s}^{2}}}$)