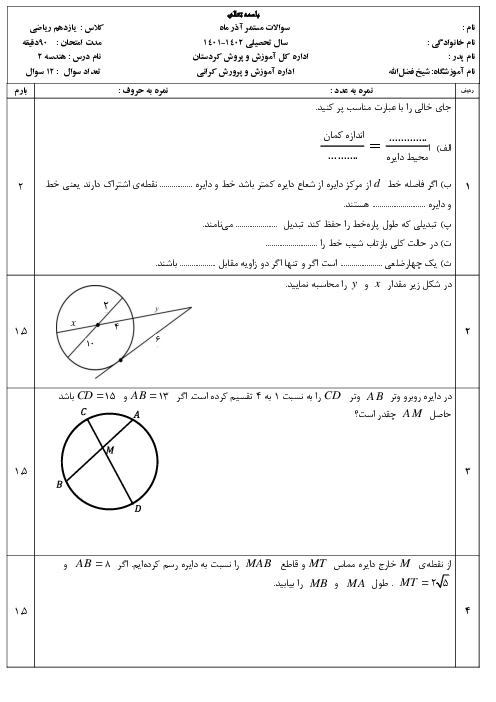
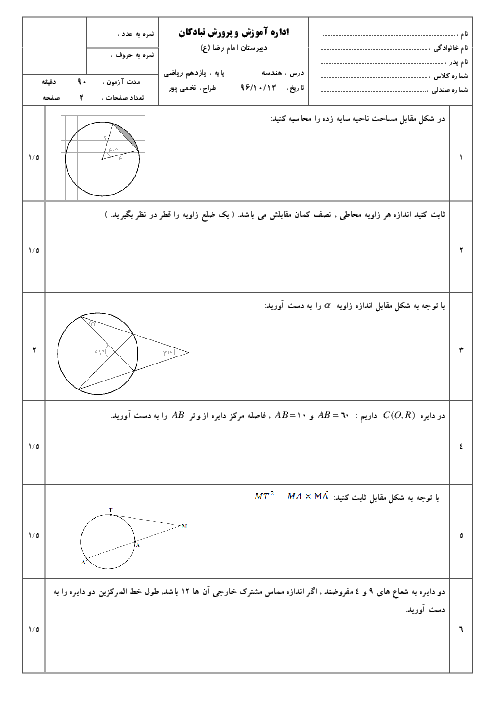
درس 3: چند ضلعیهای محاطی و محیطی
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
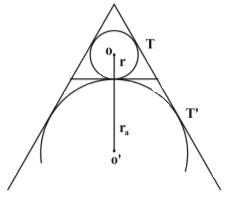
مثلث متساویالاضلاعی به ضلع $6$ واحد را در نظر بگیرید. طول مماس مشترک خارجی دو دایرهٔ محاطی داخلی و خارجی این مثلث کدام است؟