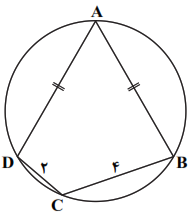
نكته‌ی 1: اگر دو ضلع يك مثلث و زاويه‌ی بين آن دو ضلع مشخص باشد، مساحت مثلث از روابط زير به‌دست می‌آيد:

$S=\frac{1}{2}bc\operatorname{Sin}\hat{A}=\frac{1}{2}ac\operatorname{Sin}\hat{B}=\frac{1}{2}ab\operatorname{Sin}\hat{C}$

نکته‌ی 2: در هر چهارضلعی محاطی، زوایای روبه‌رو مکملند.

نکته‌ی 3: بر طبق قضیه‌ی کسینوس‌ها در مثلث ABC با اضلاع a، b و c داریم:

$\left\{ \begin{matrix}
   {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\operatorname{Cos}\hat{A}  \\
   {{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\operatorname{Cos}\hat{B}  \\
   {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\operatorname{Cos}\hat{C}  \\
\end{matrix} \right.$

نکته‌ی 4: مساحت مثلث متساوی‌الاضلاع به ضلع a برابر است با:

$\frac{\sqrt{3}}{4}{{a}^{2}}$

ابتدا با توجه به نکته‌ی 1، داریم:

${{S}_{\vartriangle CBD}}=\frac{1}{2}CD\times CB\times \operatorname{Sin}\hat{C}\Rightarrow 2\sqrt{3}=\frac{1}{2}\times 2\times 4\times \operatorname{Sin}\hat{C}\Rightarrow \operatorname{Sin}\hat{C}=\frac{\sqrt{3}}{2}$

$\xrightarrow{(Monfarejeh)\,\hat{C}}\,\hat{C}={{120}^{{}^\circ }}\,\xrightarrow{Nokteyeh\,2}\,\hat{A}={{60}^{{}^\circ }}\,\xrightarrow{AB=AD}$ متساوی‌الاضلاع ABD مثلث

حال با توجه به نکته‌ی 3، در مثلث CBD، داریم:

$\begin{align}
  & B{{D}^{2}}=C{{D}^{2}}+C{{B}^{2}}-2CD\times CB\times \operatorname{Cos}{{120}^{{}^\circ }} \\ 
 & =4+16-2\times 2\times 4\times (-\frac{1}{2})=28\Rightarrow BD=\sqrt{28} \\ 
\end{align}$

و در نهایت از آن‌جایی‌که مثلث ABD متساوی‌الاضلاع است و طول ضلع آن $\sqrt{28}$ است، با توجه به نکته‌ی 4، مساحت آن برابر است با:

${{S}_{\vartriangle ABD}}=\frac{\sqrt{3}}{4}{{(\sqrt{28})}^{2}}=\frac{\sqrt{3}}{2}\times 28=7\sqrt{3}$