در شکل مقابل اگر باشد، ثابت کنید: | هندسه (3) دوازدهم شماره 262635 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول آزمون ماهانه نمونه سوال گام به گام طرح درس کاربرگ تیزهوشان هنرستان تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم‌ها

فرم معتبر نیست.

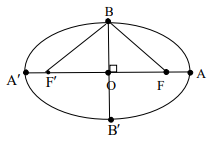
درس 3: بیضی و سهمی هندسه (3) دوازدهم متوسطه دوم نظری علوم ریاضی درسنامه آموزشی این مبحث

در شکل مقابل اگر $OF = c\,,\,OB = b\,,\,OA = a$ باشد، ثابت کنید: ${a^2} = {b^2} + {c^2}$

نمایش پاسخ

نقطه B روی عمودمنصف پاره‌خط $FF'$ قرار دارد، در نتیجه: $BF = BF'\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)$

فاصله هر نقطه روی بیضی از دو کانون برابر است با قطر بزرگ بیضی:

$BF = BF' = 2a\xrightarrow{{(1)}}BF = BF' = a$

بنابه رابطه فیثاغورث در مثلث BOF داریم:

$O{F^2} + O{B^2} = B{F^2} \to {c^2} + {b^2} = {a^2}$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

منتظریم اولین نفر تحلیلش کنه!

پاورپوینت دوره آموزشی، هندسه (3) دوازدهم متوسطه دوم نظری

مدرس: رضا زینی وند

مدت دوره: 141 اسلاید (5 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

سوپراستار

بسته ویژه نمره بیست: 18 دوره امتحان نهایی درس هندسه (3) دوازدهم

88 صفحه

بسته ویژه نمره بیست: 18 دوره امتحان نهایی درس هندسه (3) دوازدهم

ويژه نامه نوبت اول و…

سوپراستار

جزوه آموزشی، تمرین و تست هندسه 3 | فصل 3: بردارها

32 صفحه

جزوه آموزشی، تمرین و تست هندسه 3 | فصل 3: بردارها

عاصف محبی

سوالات امتحان نهایی هندسه (3) دوازدهم مدارس خارج از کشور | دی 1400 (نوبت عصر)

2 صفحه

سوالات امتحان نهایی هندسه (3) دوازدهم مدارس خارج از کشور | دی 1400 (نوبت…

محبوبه نیازی

امتحان نوبت اول دیماه 1401 هندسه 3 دوازدهم دبیرستان سلام

5 صفحه

امتحان نوبت اول دیماه 1401 هندسه 3 دوازدهم دبیرستان سلام

مرتضی جمالی ابیانه

رایـــــگان

درسنامه کامل و نکات مهم فصل 1 هندسه دوازدهم: ماتریس و کاربردها

56 صفحه

درسنامه کامل و نکات مهم فصل 1 هندسه دوازدهم: ماتریس و کاربردها

محسن قربانی جوان

آزمون نوبت اول هندسه (3) دوازدهم دبیرستان شاهد کردکوی | دی 1398

2 صفحه

آزمون نوبت اول هندسه (3) دوازدهم دبیرستان شاهد کردکوی | دی 1398

رضا پیشداد

رایـــــگان

امتحان نهایی هندسه (3) پایه دوازدهم ریاضی | جبرانی دی 1404

3 صفحه

امتحان نهایی هندسه (3) پایه دوازدهم ریاضی | جبرانی دی 1404

امتحان نهایی

آزمون نوبت دی ماه 1401 هندسه دوازدهم دبیرستان دخترانه غیردولتی سما سنندج

6 صفحه

آزمون نوبت دی ماه 1401 هندسه دوازدهم دبیرستان دخترانه غیردولتی سما سنندج

محمدجواد باغبان باشی

رایـــــگان

سؤالات امتحان نهایی درس هندسه (3) دوازدهم ریاضی | خرداد 1401

5 صفحه

سؤالات امتحان نهایی درس هندسه (3) دوازدهم ریاضی | خرداد 1401

امتحان نهایی

نمونه سؤال هندسه 3 ترم اول دبیرستان دکتر غلامحسین مصاحب دی 1403

8 صفحه

نمونه سؤال هندسه 3 ترم اول دبیرستان دکتر غلامحسین مصاحب دی 1403

بهروز ملکی

مارپیچ دو رشته‌ای: ساختار مارپیچی دِنا با دو رشته مکمل

کپسول آموزشی

مارپیچ دو رشته‌ای: ساختار مارپیچی دِنا با دو رشته مکمل
1404/07/24

اثر نور بر گیاهان؛ فتوسنتز و رشد بهتر

کپسول آموزشی

اثر نور بر گیاهان؛ فتوسنتز و رشد بهتر
1404/07/23

زندگی در نواحی استوایی: زندگی قبایل بومی در جنگل‌های انبوه استوایی

کپسول آموزشی

زندگی در نواحی استوایی: زندگی قبایل بومی در جنگل‌های انبوه استوایی
1404/08/11

کسرهای بین دو کسر

کپسول آموزشی

کسرهای بین دو کسر
1404/09/9

سطح جداکننده دو محیط: مرزی که دو محیط شفاف متفاوت را از هم جدا می‌کند.

کپسول آموزشی

سطح جداکننده دو محیط: مرزی که دو محیط شفاف متفاوت را از هم جدا می‌کند.
1404/10/14

عبارت گویا: کسری که صورت و مخرج آن چندجمله‌ای باشد.

کپسول آموزشی

عبارت گویا: کسری که صورت و مخرج آن چندجمله‌ای باشد.
1404/09/13

خلاصه کتاب انسان تنها با خودش نوشته فردریش نیچه ترجمه میلاد یساول

خلاصه کتاب

خلاصه کتاب انسان تنها با خودش نوشته فردریش نیچه ترجمه میلاد یساول
1404/05/27

مصرف‌کننده گوشتخوار: جانوری که از جانوران دیگر تغذیه می‌کند.

کپسول آموزشی

مصرف‌کننده گوشتخوار: جانوری که از جانوران دیگر تغذیه می‌کند.
1404/10/2

سیستم ایمنی: مجموعه دفاعی بدن که در اثر کم‌خوابی تضعیف می‌شود

کپسول آموزشی

سیستم ایمنی: مجموعه دفاعی بدن که در اثر کم‌خوابی تضعیف می‌شود
1404/10/6

جداسازی ماسه و نمک: نمونه‌ای از جداسازی اجزای مخلوط با حل کردن و صاف‌کردن

کپسول آموزشی

جداسازی ماسه و نمک: نمونه‌ای از جداسازی اجزای مخلوط با حل کردن و صاف‌کردن
1404/10/3

موارد بیشتر

موارد بیشتر

ارسال فایل

در یک دوازده وجهی زاویه بین 2 صفحه‌اش چقدر است؟

درستی یا نادرستی ماتریس مربعی با قطر اصلی صفر

خروج از مرکز بیضی با قطرهای 10 و 6

موارد بیشتر

ارسال پرسش

موارد بیشتر