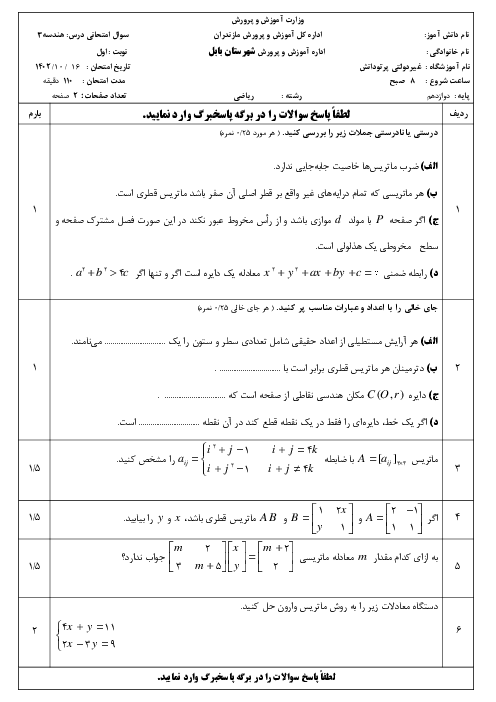
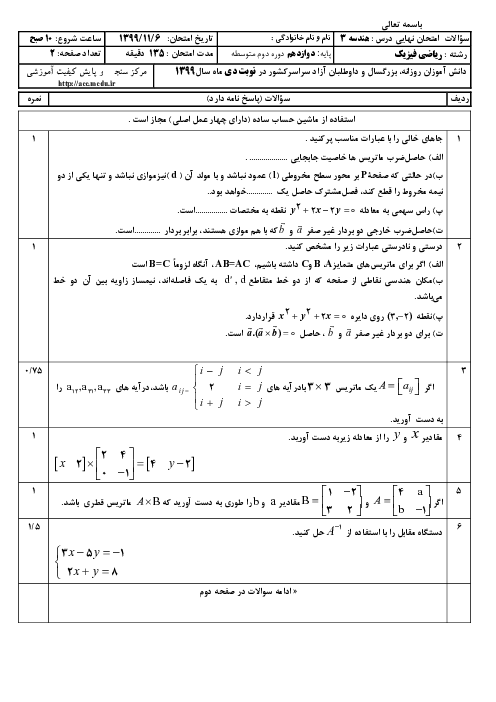
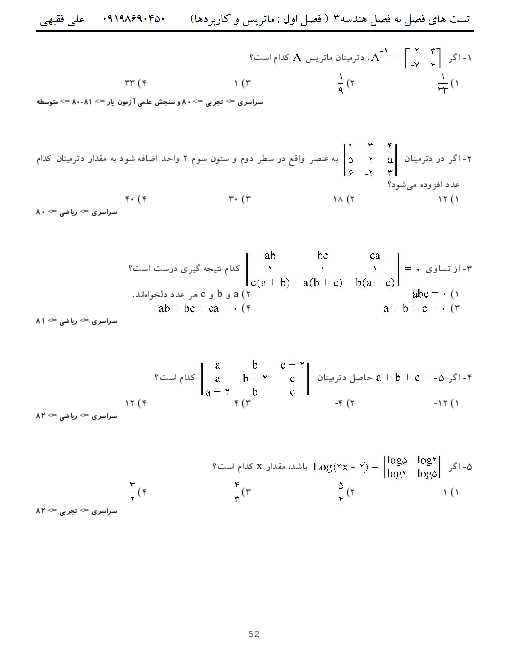
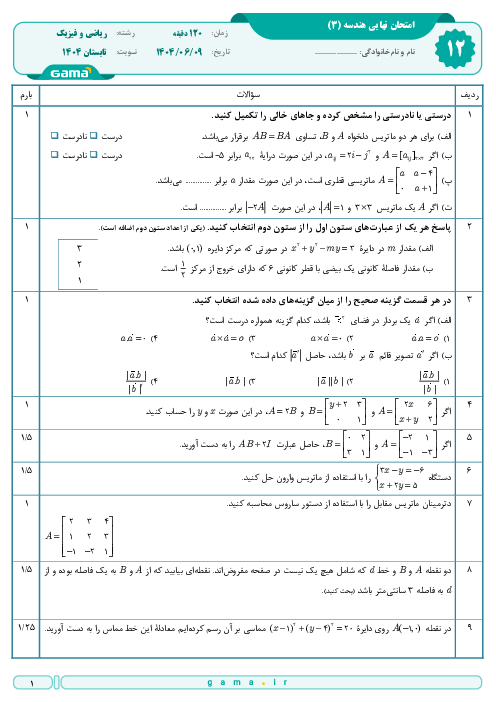
نسبت به سطر دوم دترمینان می‌گیریم:

 $\left| A \right|=\left[ \begin{matrix}
   -1 & 2 & 3  \\
   \overset{-}{\mathop{\left| A \right|}}\, & \overset{+}{\mathop{0}}\, & \overset{\_}{\mathop{-1}}\,  \\
   3 & 2\left| A \right| & 1  \\
\end{matrix} \right]=-\left| A \right|\left| \begin{matrix}
   2 & 3  \\
   2\left| A \right| & 1  \\
\end{matrix} \right|+\left| \begin{matrix}
   -1 & 2  \\
   3 & 2\left| A \right|  \\
\end{matrix} \right|$

بنابراین:

 $\begin{align}
  & \left| A \right|=-\left| A \right|(2-6\left| A \right|)+(-2\left| A \right|-6) \\
 & \Rightarrow \left| A \right|=6{{\left| A \right|}^{2}}-2\left| A \right|-2\left| A \right|-6 \\
 & \Rightarrow 6{{\left| A \right|}^{2}}-5\left| A \right|-6=0\Rightarrow (3\left| A \right|+2)(2\left| A \right|-3)=0 \\
\end{align}$

پس:

$\left\{ \begin{matrix}
   \left| A \right|=-\frac{2}{3}  \\
   \left| A \right|=\frac{3}{2}  \\
\end{matrix} \right.$