نكته: گاهی برای اثبات یک گزاره لازم است همۀ موارد ممكن در مورد مسئله را در نظر بگیریم، به این روش «اثبات با در نظر گرفتن همۀ حالتها» میگوییم.
مثال: برای هر دو عدد حقیقی $a$ و $b$ اگر $ab=0$، آنگاه $a=0$ یا $b=0$
اثبات: برای $b$ دو حالت ممكن است رخ دهد:
الف) اگر $b=0$، حكم برقرار است؛ زیرا در اینصورت گزارهٔ «$b=0\vee a=0$» درست است.
ب) اگر $b\ne 0$، طرفین عبارت را در ${{b}^{-1}}$ (یا $\frac{1}{b}$) ضرب میکنیم:
$ab=0\Rightarrow \frac{1}{b}(ab)=0\Rightarrow a=0$
پس حكم برقرار است.
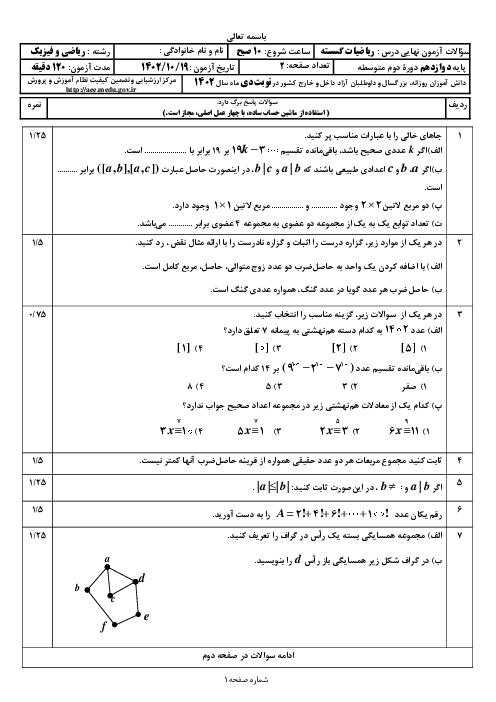
بنابراین گزینۀ $3$ پاسخ است.