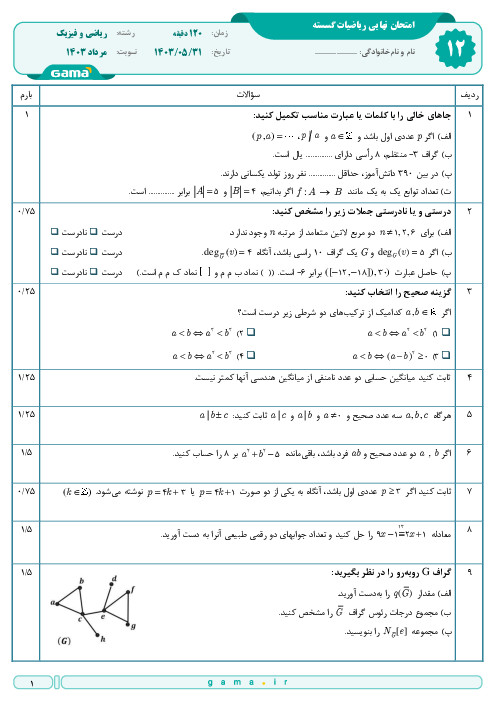
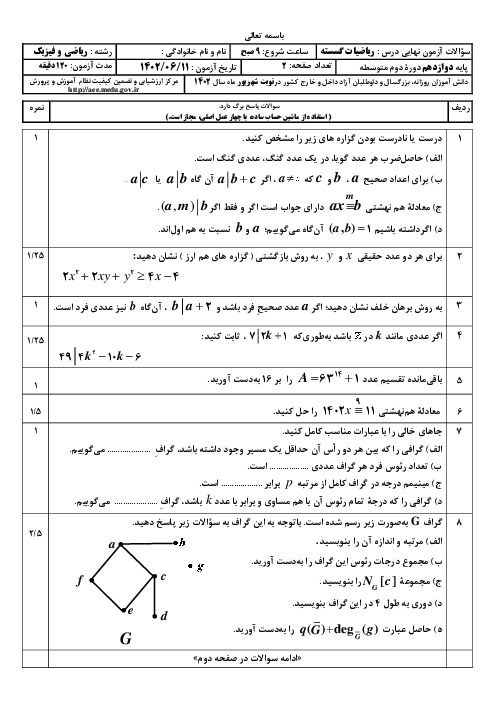
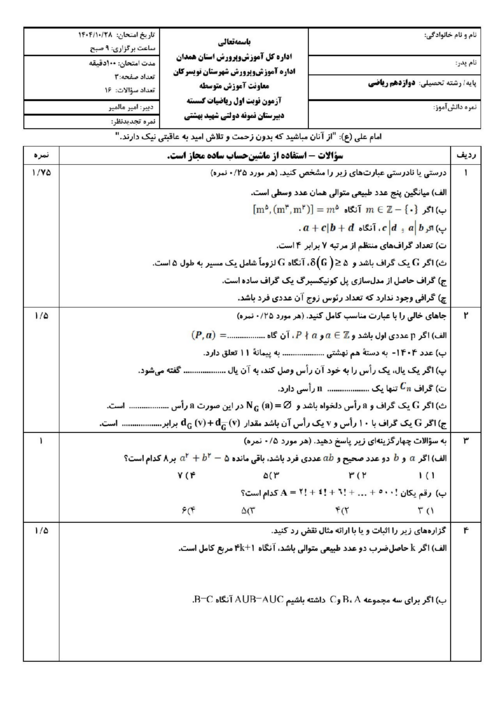
${a_1},{a_2},{a_3}$ اعدادی صحیح هستند و ${b_1},{b_2},{b_3}$ هم همان اعداد ولی به ترتیب دیگری قرار گرفته اند. ثابت کنید $({a_1} - {b_1})({a_2} - {b_2})({a_3} - {b_3})$ عددی زوج است.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...