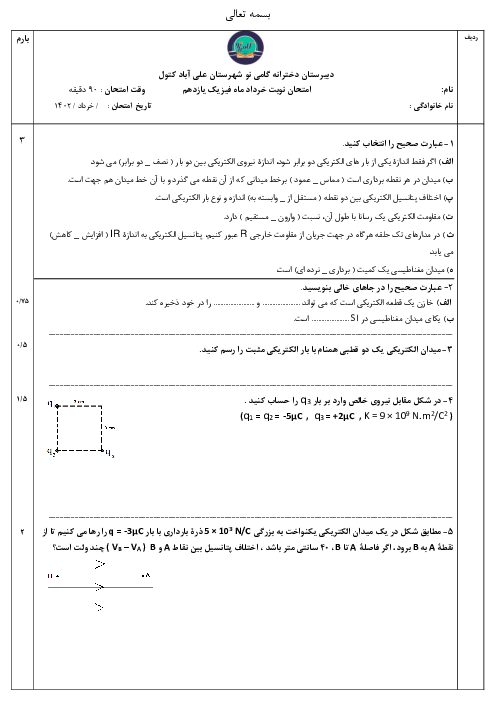
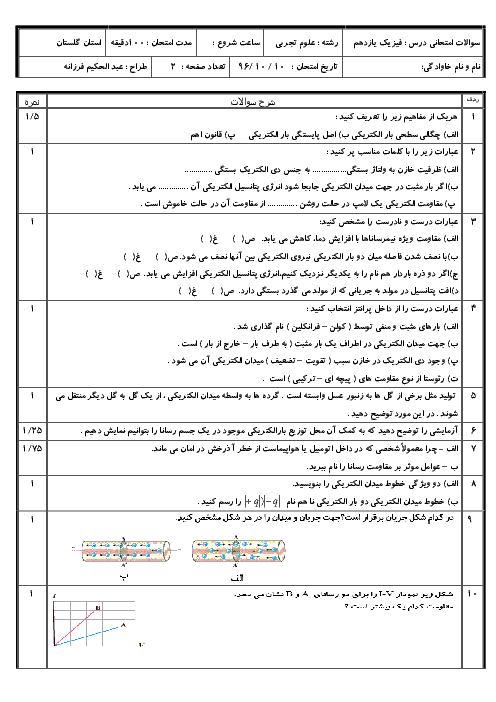
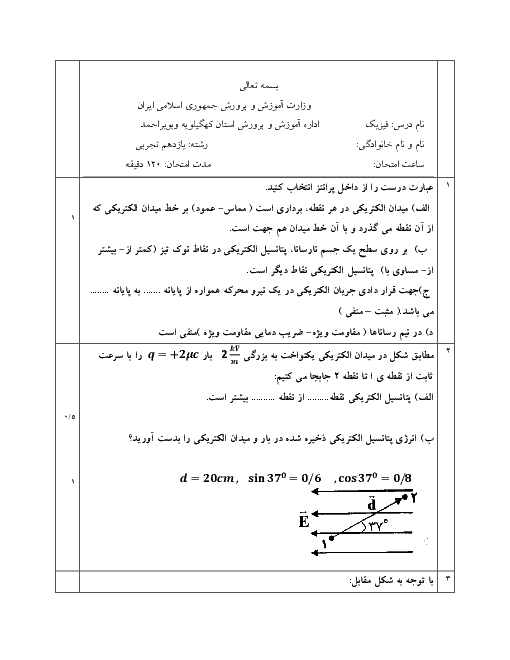
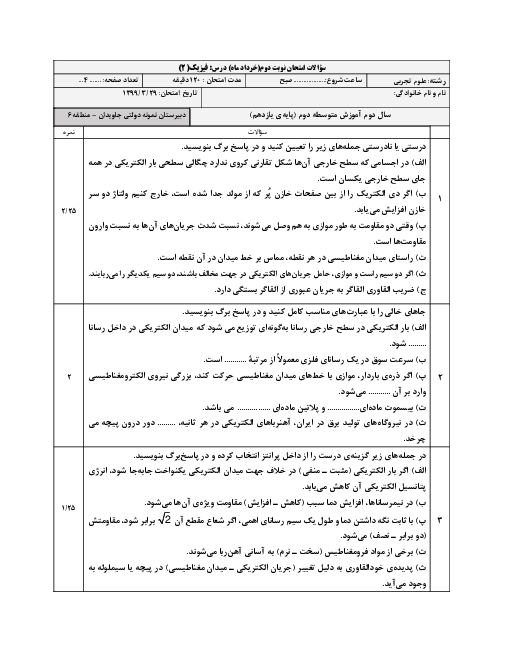
ابتدا شار مغناطیسی عبوری از حلقه را در لحظات ${{t}_{1}}=1s$، ${{t}_{2}}=2s$ و ${{t}_{3}}=3s$ به دست می‌آوریم:

$\Phi ={{t}^{2}}+t\Rightarrow \left\{ \begin{matrix} {{t}_{1}}=1s\Rightarrow {{\Phi }_{1}}=2Wb  \\ {{t}_{2}}=2s\Rightarrow {{\Phi }_{2}}=6Wb  \\ {{t}_{3}}=3s\Rightarrow {{\Phi }_{3}}=12Wb  \\ \end{matrix} \right.$

در ادامه بزرگی تغییرات شار مغناطیسی گذرنده از حلقه را در ثانیه‌های دوم و سوم به دست می‌آوریم:

$\Delta {{\Phi }_{2-1}}=6-2=4Wb$

$\Delta {{\Phi }_{3-2}}=12-6=6Wb$

با توجه به روابط زیر می‌توانیم نتیجه بگیریم که اندازه‌ی جریان القایی متوسط، متناسب با اندازه‌ی تغییرات شار مغناطیسی عبوری از حلقه است. بنابراین داریم:

$\overline{I}=\frac{\left| \varepsilon  \right|}{R}=\frac{1}{R}\left| \frac{N\Delta \Phi }{\Delta t} \right|\xrightarrow{\Delta {{t}_{1}}=\Delta {{t}_{2}}}\frac{\overline{{{I}_{2}}}}{\overline{{{I}_{1}}}}=\frac{\Delta {{\Phi }_{2}}}{\Delta {{\Phi }_{1}}}\Rightarrow \frac{\overline{{{I}_{2}}}}{8}=\frac{6}{4}\Rightarrow {{I}_{2}}=12A$