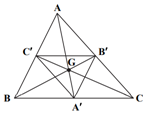
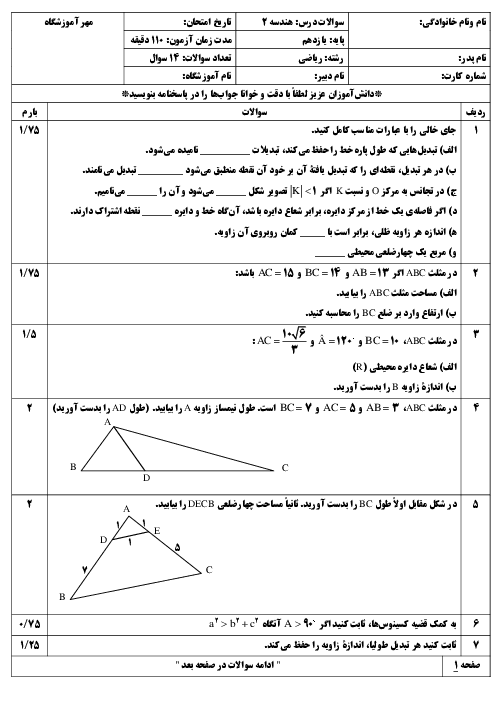
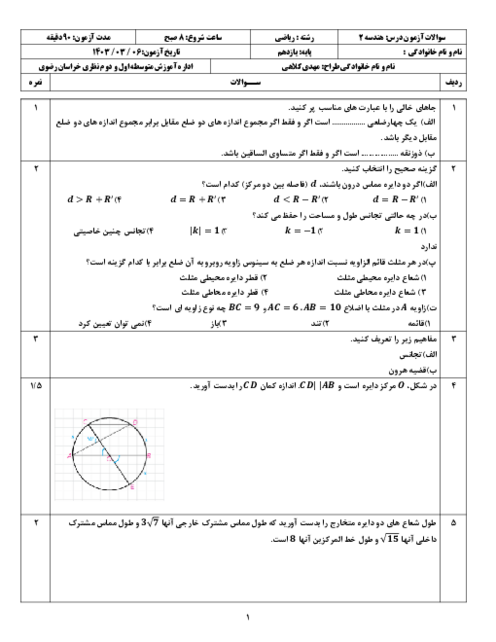
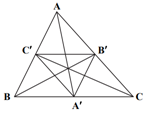
«در شكل مقابل ${A}'$، ${B}'$ و ${C}'$ وسط اضلاع مثلث $ABC$ هستند. مثلث $ABC$ با يک تجانس به مركز ............... و نسبت ................ روی مثلث ${A}'{B}'{C}'$ تصوير می‌شود.» جملۀ بالا با كدام گزينه به‌درستی كامل می‌شود؟
1 )
مركز ثقل مثلث $ABC$، $+\frac{1}{2}$
مركز ثقل مثلث $ABC$، $-\frac{1}{2}$
3 )
یکی از رئوس مثلث $ABC$، $+\frac{1}{2}$
4 )
یکی از رئوس مثلث $ABC$، $-\frac{1}{2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...