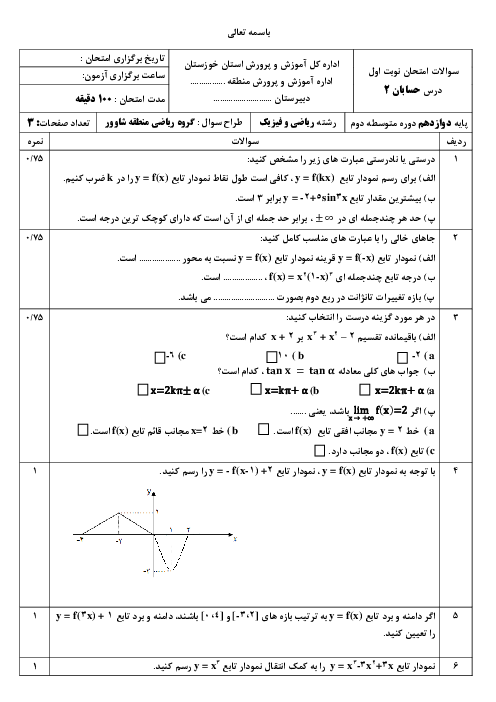
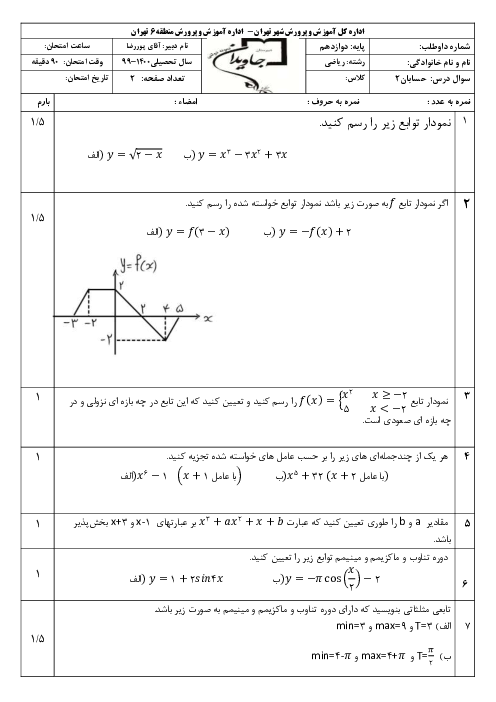
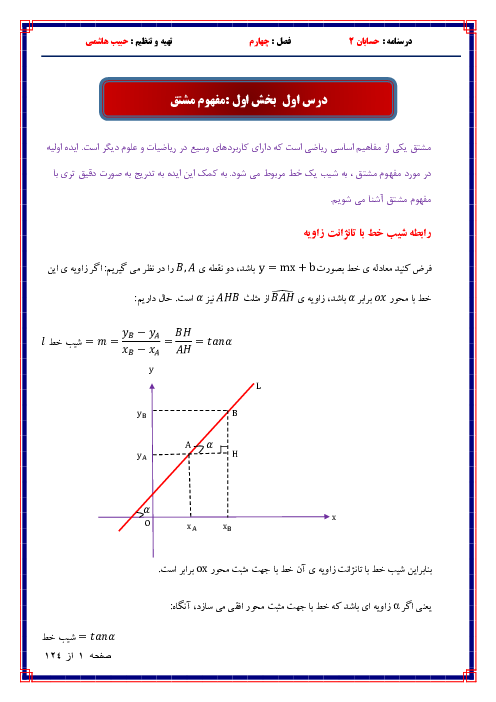
درس 3: آهنگ متوسط تغییر و آهنگ لحظه‌ای تغییر
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
تابع $f(x) = \frac{1}{3}{x^3} - 4x + 1$ مفروض است. در نقطهٔ $x = a$، آهنگ تغییر لحظه‌ای تابع کمتر از آهنگ تغییر متوسط آن در بازه $[0\,,\,3]$ است، محدوده $a$ را بیابید.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...