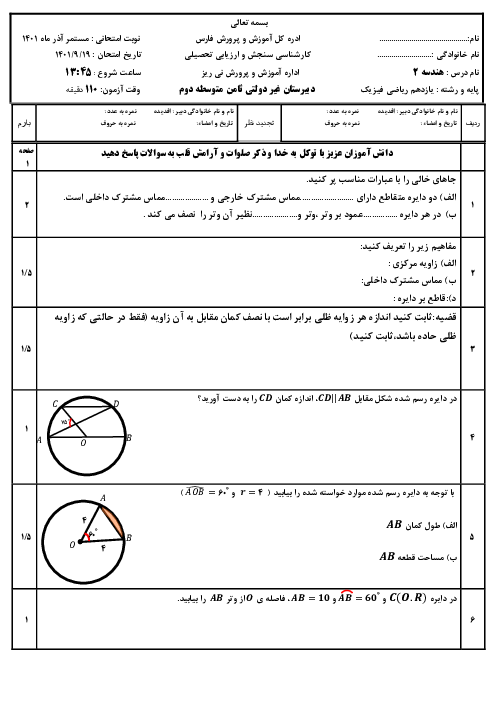
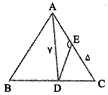
در مثلث متساوی الاضلاع ABC به ضلع 8 واحد، نقطه D به فاصله 7 واحد از رأس A قرار دارد و نقطه E به فاصله 5 واحد از C قرار دارد$(CD>BD)$. اندازه پاره خط CD و زاویه AED چند درجه است؟
$A\hat{E}D={{120}^{\circ }},CD=5$
2 )
$A\hat{E}D={{100}^{\circ }},CD=3$
3 )
$A\hat{E}D={{120}^{\circ }},CD=3$
4 )
$A\hat{E}D={{100}^{\circ }},CD=4$
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...