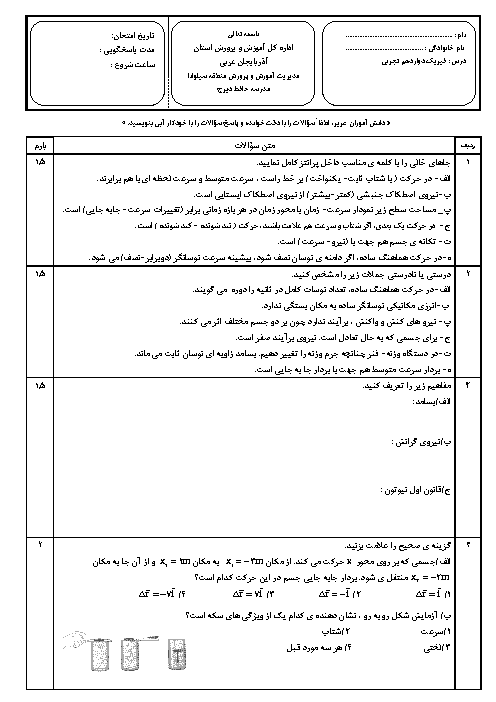
قسمت 3: حرکت با شتاب ثابت
فیزیک (3) تجربی
دوازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
نمودار شتاب – مكان متحرکی كه روی محور $x$ حركت میكند، مطابق شكل زير است. اگر متحرک در لحظهٔ $t=0$ از مبدأ مکان با سرعت $8$ متر بر ثانیه عبور كند، سرعت متوسط آن در بازهای كه حركت آن تندشونده است، چند متر بر ثانيه است؟