از یک سیم‌‌لولهٔ آرمانی، جریان متناوب سینوسی که نمودار تغییرات آن برحسب زمان به صورت شکل زیر است، عبور می‌کند. اگر انرژی ذخیره‌شده در سیملوله در لحظهٔ ثانیه برابر…

مغناطیس، الکترومغناطیس و جریان متناوب فیزیک کنکور سراسری دوره دوم متوسطه- نظری علوم ریاضی

از یک سیم‌‌لولهٔ آرمانی، جریان متناوب سینوسی که نمودار تغییرات آن برحسب زمان به صورت شکل زیر است، عبور می‌کند. اگر انرژی ذخیره‌شده در سیملوله در لحظهٔ $\frac{1}{{400}}$ ثانیه برابر 72 میلی‌ژول باشد، ضریب القاوری (خودالقایی) سیملوله چند میلی‌هانری است؟

1 )

2 )

3 )

4 )

نمایش پاسخ

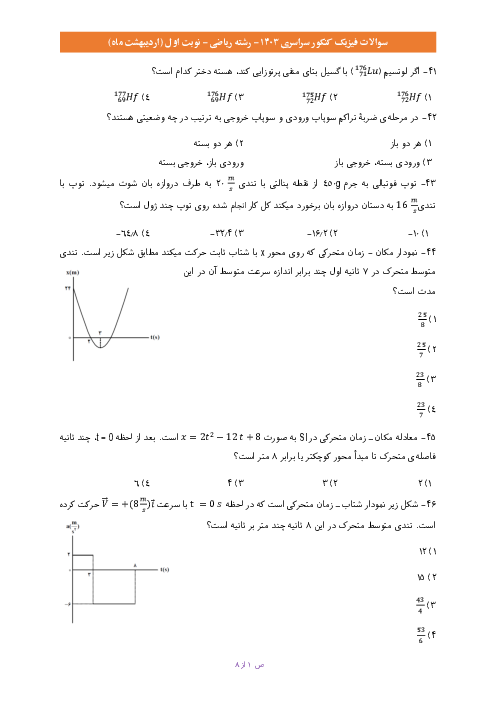
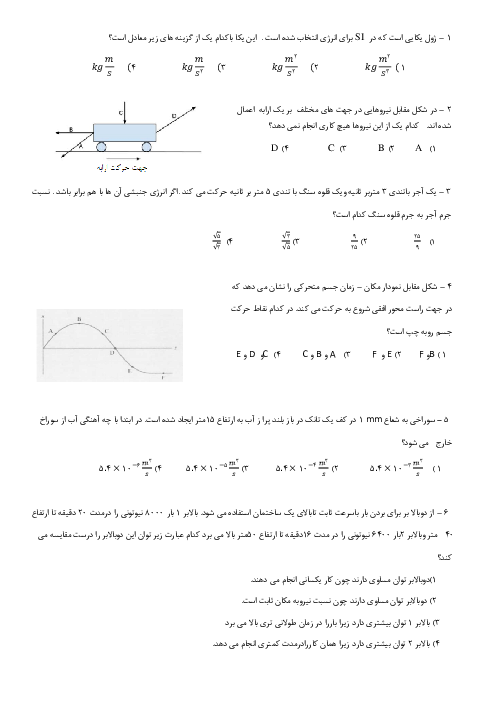
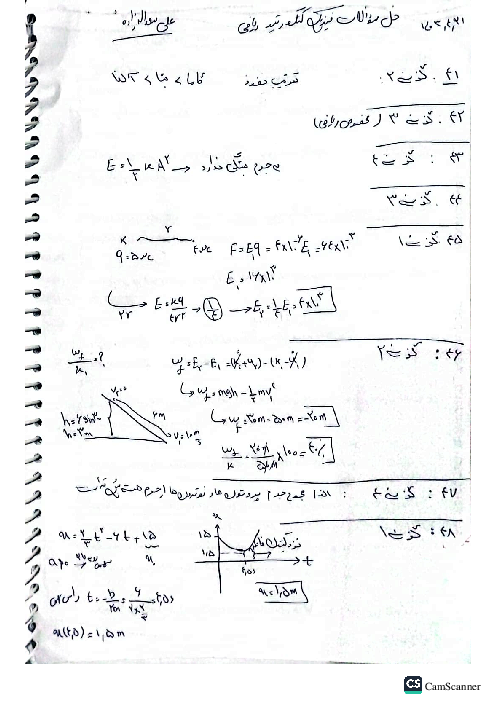
گام اول: ابتدا معادلهٔ جریان را با استفاده از اطلاعات نمودار می‌نویسیم:

$\frac{5}{4}T = \frac{1}{{40}} \Rightarrow T = \frac{1}{{50}}s,{I_m} = 6A$

$I = {I_m}\sin (\frac{{2\pi }}{T}t) = 6\sin (\frac{{2\pi }}{{\frac{1}{{50}}}}t) = 6\sin (100\pi t)$

گام دوم: جریان در لحظهٔ $t = \frac{1}{{400}}s$ برابر است با:

$I = 6\sin (100\pi t) = 6\sin (100\pi \times \frac{1}{{400}}) = 6\sin (\frac{\pi }{4})$

$= 3\sqrt 2 A$

گام سوم: از رابطهٔ $U = \frac{1}{2}L{I^2}$ ، ضریب القاوری سیم‌لوله را به دست می‌آوریم:

$U = \frac{1}{2}L{I^2} \Rightarrow 72 \times {10^{ - 3}} = \frac{1}{2} \times L \times {(3\sqrt 2 )^2}$

$\Rightarrow L = 8 \times {10^{ - 3}}H \Rightarrow L = 8mH$

گزارش اشکال

جستجوهای پرتکرار

پاسخ تشریحی :

تحلیل ویدئویی تست

با گنجینه سوال

روانشناسی

اقتصاد

زبان عربی تخصصی

زبان عربی (تا 1401)

فیزیک

زیست شناسی

ریاضیات

زبان و ادبیات فارسی تخصصی

زمین شناسی

فلسفه و منطق کنکور

آزمون سراسری زبان

زبان و ادبیات فارسی (تا 1401)

ریاضی

فیزیک

شیمی

علوم اجتماعی

تاریخ و جغرافیا (تا 1401)

آزمون سراسری هنر

فرهنگ و معارف اسلامی (تا 1401)

زبان انگلیسی (تا 1401)

نمونه سوالات مشابه

اطلاع از تغییرات در بسته‌های گاما

کاربر عزیز سلام!

پاسخ تشریحی :

تحلیل ویدئویی تست

با گنجینه سوال

روانشناسی

اقتصاد

زبان عربی تخصصی

زبان عربی (تا 1401)

فیزیک

زیست شناسی

ریاضیات

زبان و ادبیات فارسی تخصصی

زمین شناسی

فلسفه و منطق کنکور

آزمون سراسری زبان

زبان و ادبیات فارسی (تا 1401)

ریاضی

فیزیک

شیمی

علوم اجتماعی

تاریخ و جغرافیا (تا 1401)

آزمون سراسری هنر

فرهنگ و معارف اسلامی (تا 1401)

زبان انگلیسی (تا 1401)

نمونه سوالات مشابه