درس 2: معادلهٔ درجهٔ دوم و تابع درجه 2
ریاضی (2)
یازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
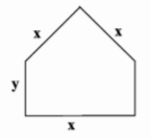
محیط پنجرهای به شکل مقابل 4/2 متر است. به ازای کدام مقدار x، این پنجره بیشترین نوردهی را دارد؟