درس 2: معادلهٔ درجهٔ دوم و تابع درجه 2
ریاضی (2)
یازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
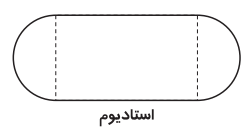
استاديومی به شكل مستطيل با دو نيم دايره در دو انتهای آن در حال ساخت است. اگر محيط استاديوم 1500 متر باشد، طول مستطيل چقـدر باشد تا مساحت مستطيل حداكثر مقدار ممكن شود؟
تحلیل ویدئویی تست
یوسف شاکر اردکانی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...