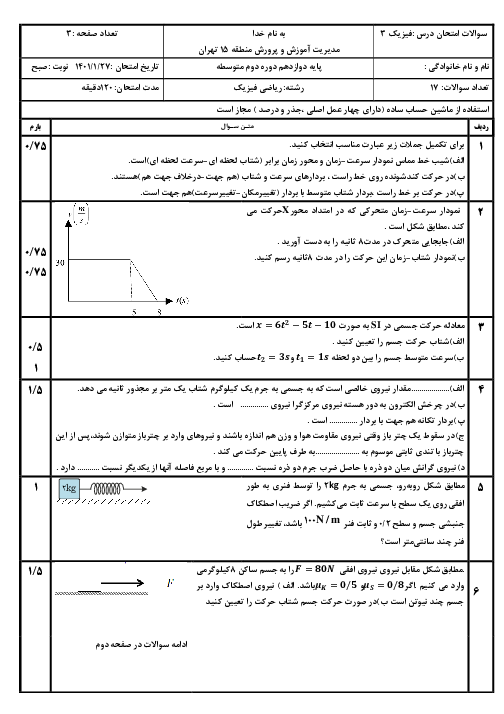
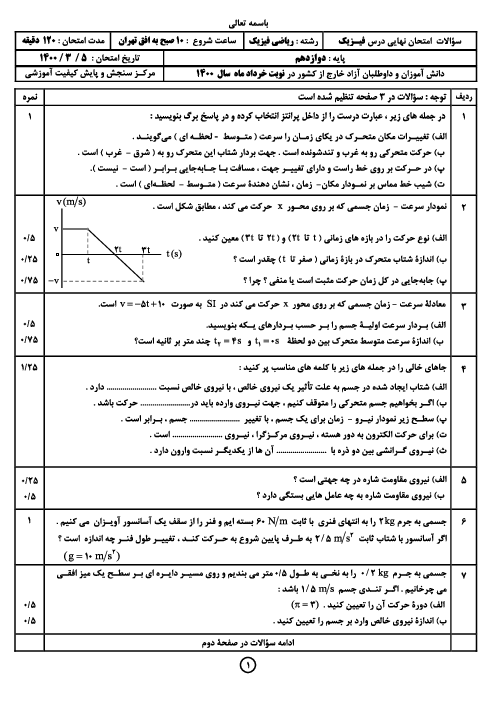
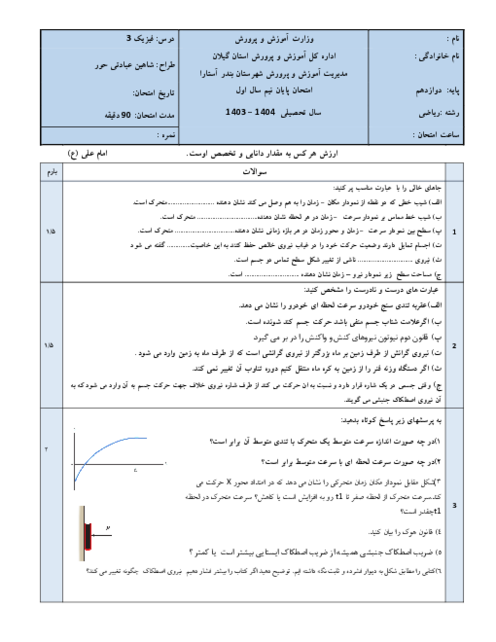
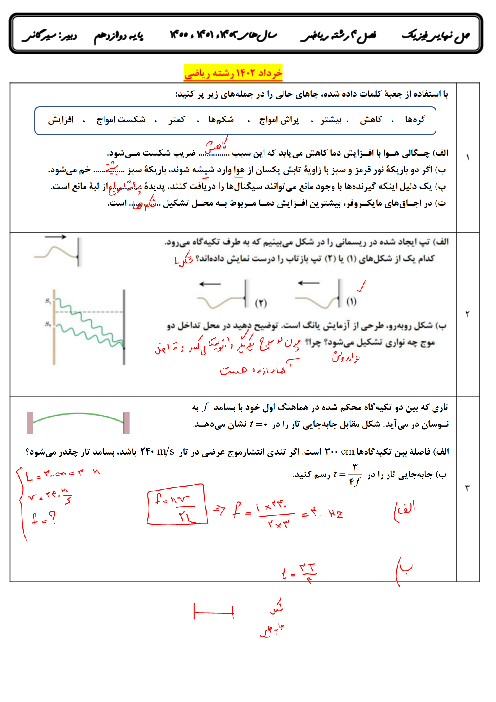
یک گلوله به جرم به انتهای ریسمانی به طول و جرم ناچیز آویخته شده است (آونگ ساده). گلوله با انحراف کمی از راستای قائم به نوسان درمی آید و در هر دقیقه نوسان انجام… | فیزیک (3) ریاضی دوازدهم شماره 82069

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

** فصل 3: نوسان و موج فیزیک (3) ریاضی دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

یک گلوله به جرم $m$ به انتهای ریسمانی به طول $L$ و جرم ناچیز آویخته شده است (آونگ ساده). گلوله با انحراف کمی از راستای قائم به نوسان درمی آید و در هر دقیقه $20$ نوسان انجام می‌دهد. اگر بخواهیم آونگ در هر دقیقه $30$ نوسان انجام دهد، می‌توانیم ............... (از همه‌ی اصطکاک ها چشم‌پوشی نمایید و ${{R}_{e}}$ شعاع زمین است.)

1 )

از گلوله با جرم $\frac{4}{9}m$ استفاده کنیم.

2 )

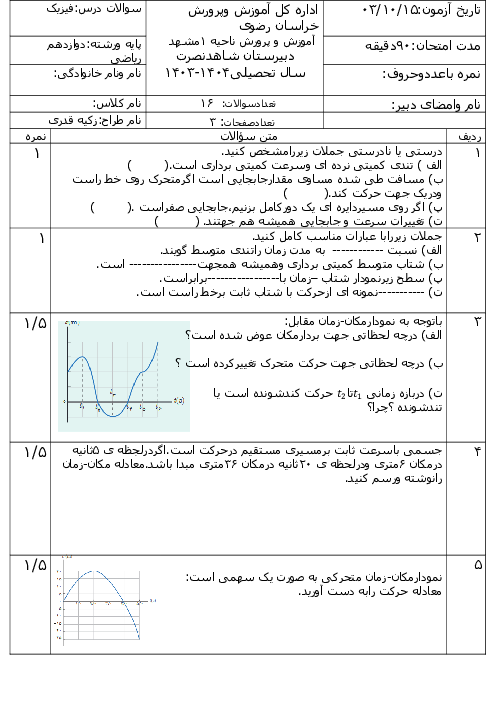
از ریسمان با طول $\frac{4}{9}L$ استفاده کنیم.

3 )

آونگ را با انحراف کمتری از راستای قائم به نوسان درآوریم.

4 )

آونگ را در فاصله‌ی $\frac{1}{2}{{R}_{e}}$ از سطح زمین به نوسان درآوریم.

نمایش پاسخ

دوره و بسامد آونگ ساده، به جرم وزنه و دامنه‌ی نوسان بستگی ندارد. پس گزینه‌های (1) و (3) اثری در بسامد و در نتیجه تعداد نوسان آونگ ساده در هر دقیقه ندارند.

با دور شدن از سطح زمین، گرانش ضعیف‌تر و g کمتر می‌شود $(g=\frac{G{{M}_{e}}}{{{({{R}_{e}}+h)}^{2}}})$ و طبق رابطه‌ی $T=2\pi \sqrt{\frac{L}{g}}$ دوره‌ی آونگ بیشتر و تعداد نوسان آن کمتر می‌شود. (گزینه‌ی 4 نادرست است.)

گزینه‌ی 2 پاسخ درست است؛ زیرا:

${{L}_{2}}=\frac{4}{9}{{L}_{1}}\xrightarrow{T=2\pi \sqrt{\frac{L}{g}}}{{T}_{2}}=\frac{2}{3}{{T}_{1}}\xrightarrow{N=\frac{\Delta t}{T}}{{N}_{2}}=\frac{3}{2}{{N}_{1}}=\frac{3}{2}\times 20=30$

گزارش اشکال