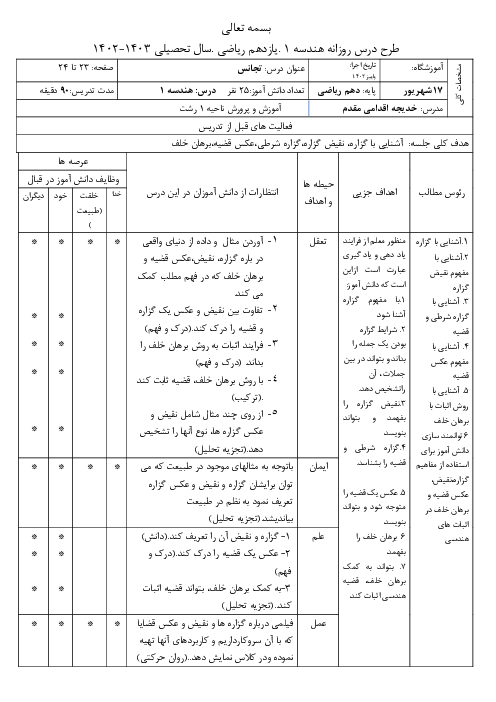
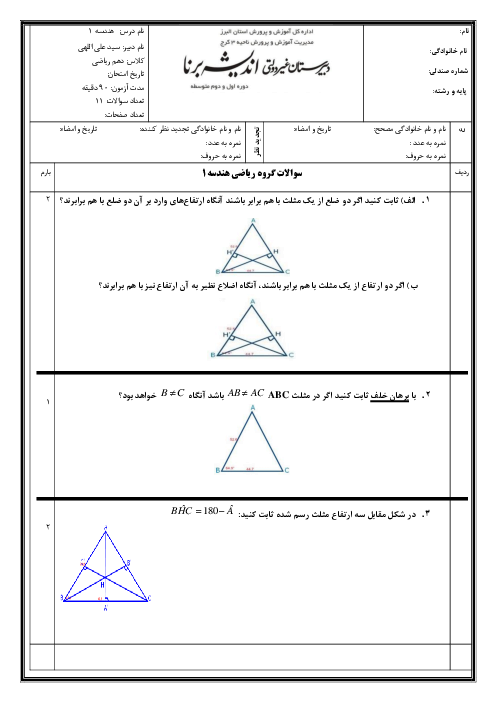
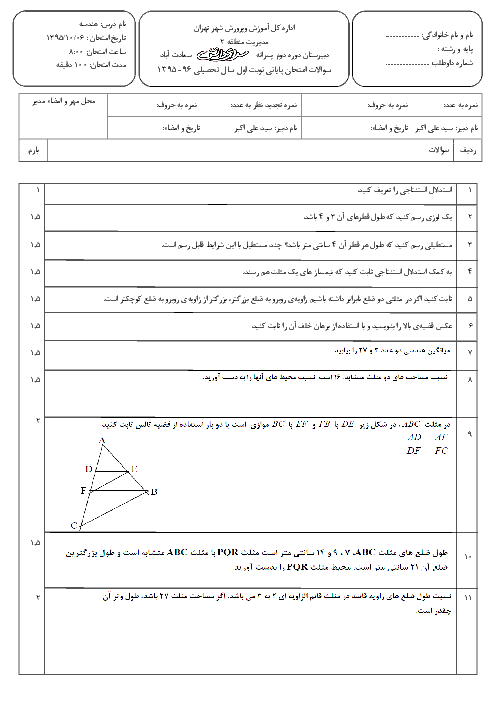
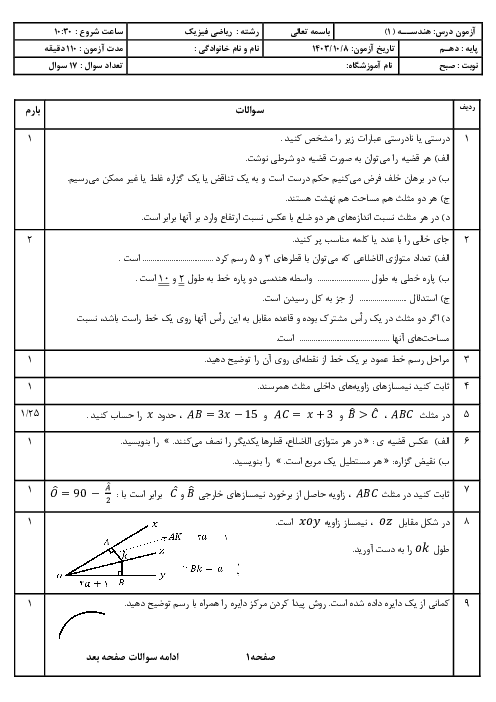
اگر $\frac{a}{b}=\frac{c}{d}$ باشد، کدام رابطه برقرار است؟ $(m,n\in \mathbb{Z},x,y\in \mathbb{R})$
1 )
${{(\frac{ma+nc}{mb+nd})}^{2}}={{(\frac{ax}{by})}^{2}}$
2 )
${{(\frac{ma+nc}{nb+md})}^{3}}=\frac{{{(ax)}^{3}}+{{(cy)}^{3}}}{{{(bx)}^{3}}+{{(dy)}^{3}}}$
3 )
$\frac{{{a}^{2}}+{{c}^{2}}}{{{b}^{3}}+{{d}^{3}}}={{(\frac{ma+nc}{mb+nd})}^{\frac{2}{3}}}$
${{(\frac{ma+nc}{mb+nd})}^{\frac{3}{2}}}=\frac{{{(ax)}^{\frac{3}{2}}}+{{(cy)}^{\frac{3}{2}}}}{{{(bx)}^{\frac{3}{2}}}+{{(dy)}^{\frac{3}{2}}}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...