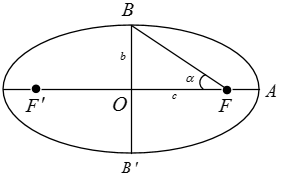
فاصلهٔ $A$ تا ${A}'$ برابر با قطر بزرگ بیضی یعنی $2a$ است، پس:
$2a=(-2+\sqrt{3})-(-2-\sqrt{3})=2\sqrt{3}\Rightarrow a=\sqrt{3}$
نسبت قطر کوچک به قطر بزرگ بیضی برابر با $\frac{2b}{2a}$ یعنی $\frac{b}{a}$ است، بنابراین:
$\frac{b}{a}=\frac{1}{2}\xrightarrow{a=\sqrt{3}}b=\frac{\sqrt{3}}{2}$
به کمک رابطهٔ ${{a}^{2}}-{{c}^{2}}={{b}^{2}}$ داریم:
${{(\sqrt{3})}^{2}}-{{c}^{2}}={{(\frac{\sqrt{3}}{2})}^{2}}\Rightarrow c=\frac{3}{2}$
با توجه به شکل پایین صفحه، تانژانت زاویهٔ $\alpha $ برابر است با:
$\tan \alpha =\frac{b}{c}=\frac{\frac{\sqrt{3}}{2}}{\frac{3}{2}}=\frac{\sqrt{3}}{3}\Rightarrow \alpha ={{30}^{\circ }}$
پس زاویهٔ $BF{B}'$ برابر با $2\alpha =2\times {{30}^{\circ }}={{60}^{\circ }}$ است.