درس 3: چند ضلعی‌های محاطی و محیطی
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
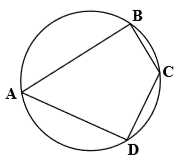
در شکل مقابل، $\hat{C}-2\hat{A}={{12}^{\circ }}$. اندازهٔ $\hat{B}+\hat{C}+\hat{D}$ کدام است؟
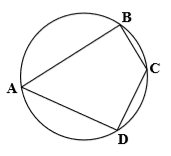
1 )
${{214}^{\circ }}$
2 )
${{204}^{\circ }}$
${{304}^{\circ }}$
4 )
${{314}^{\circ }}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...