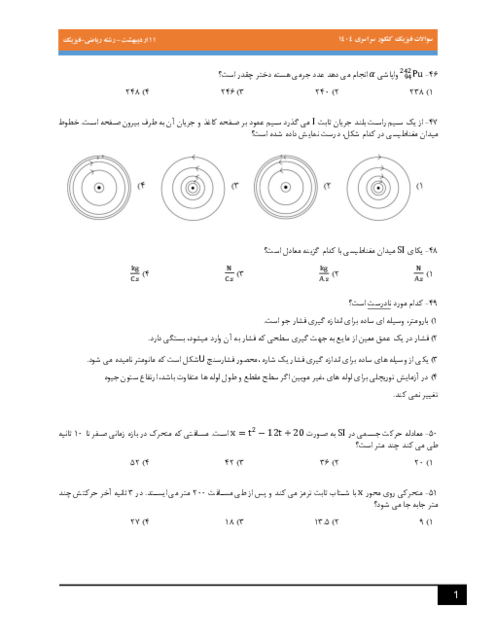
نوسانگری روی پارهخطی به طول 8cm روی سطح افقی بدون اصطکاک، حرکت هماهنگ ساده انجام میدهد. اگر در لحظهای که فاصله نوسانگر از نقطه تعادل برابر 2cm است بزرگی شتاب برابر $\frac{{{\pi ^2}}}{2}\frac{m}{{{s^2}}}$ باشد، تندی نوسانگر در لحظه عبور از نقطهٔ تعادل چند متر بر ثانیه است؟