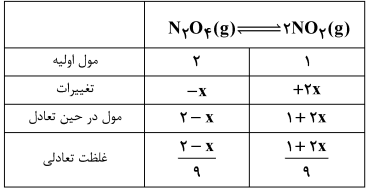
ابتدا ثابت تعادل را می‌یابیم (چون با تغییر حجم ظرف، ثابت تعادل تغییری نخواهد کرد.)

$\begin{align}
  & ?mol{{N}_{2}}{{O}_{4}}=184g{{N}_{2}}{{O}_{4}}\times \frac{1mol{{N}_{2}}{{O}_{4}}}{92g{{N}_{2}}{{O}_{4}}}=2mol{{N}_{2}}{{O}_{4}} \\ 
 & {{N}_{2}}{{O}_{4}}ghelzat=\frac{2}{0/5}=4mol.{{L}^{-1}} \\ 
 & ?molN{{O}_{2}}=46gN{{O}_{2}}\times \frac{1molN{{O}_{2}}}{46N{{O}_{2}}}=1molN{{O}_{2}} \\ 
 & N{{O}_{2}}ghelzat=\frac{1}{0/5}=2mol.{{L}^{-1}} \\ 
 & K=\frac{{{\left[ N{{O}_{2}} \right]}^{2}}}{\left[ {{N}_{2}}{{O}_{4}} \right]}=\frac{{{(2)}^{2}}}{4}=1\frac{mol}{L} \\ 
\end{align}$ 

با افزایش حجم ظرف به 9 لیتر، تعادل به سمت مول گازی بیش‌تر (در جهت رفت) جابه‌جا خواهد شد:

$\begin{align}
  & K=\frac{{{\left[ N{{O}_{2}} \right]}^{2}}}{\left[ {{N}_{2}}{{O}_{4}} \right]}=1\Rightarrow \frac{{{(\frac{1+2x}{9})}^{2}}}{(\frac{2-x}{9})}=1 \\ 
 & \Rightarrow 4{{x}^{2}}+13x-17=0\Rightarrow \left\{ \begin{matrix}
   x=1ghgh  \\
   x=-\frac{17}{4}ghghgh  \\
\end{matrix} \right. \\ 
 & mol{{N}_{2}}{{O}_{4}}=2-x\xrightarrow{x=1}mol{{N}_{2}}{{O}_{4}}=1 \\ 
 & ?g{{N}_{2}}{{O}_{4}}=1mol{{N}_{2}}{{O}_{4}}\times \frac{92g{{N}_{2}}{{O}_{4}}}{1mol{{N}_{2}}{{O}_{4}}}=92g{{N}_{2}}{{O}_{4}} \\ 
\end{align}$