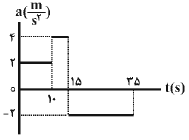
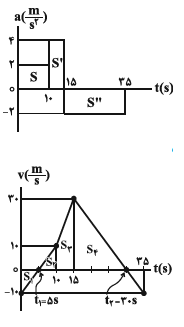
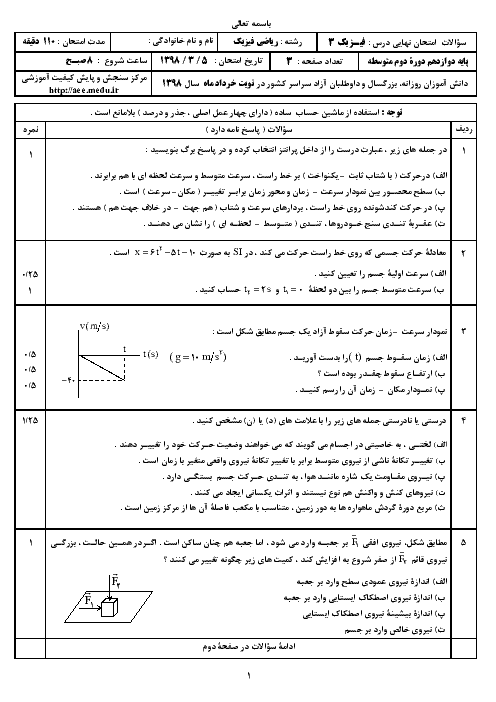
می‌دانيم سطح زير نمودار شتاب – زمان برابر با تغييرات سرعت است، بنابراين داريم:

$_{(10s-15s):\Delta v={S}'\Rightarrow {{v}_{15}}-{{v}_{10}}=5\times 4\xrightarrow{{{v}_{10}}=-10\frac{m}{s}}{{v}_{15}}=30\frac{m}{s}}^{(0-10s):\Delta v=S\Rightarrow {{v}_{10}}-{{v}_{0}}=20\xrightarrow{{{v}_{0}}=-10\frac{m}{s}}{{v}_{10}}=10\frac{m}{s}}$ 

$(15s-35s):\Delta v={S}''\Rightarrow {{v}_{35}}-{{v}_{15}}=-2\times 20\xrightarrow{{{v}_{15}}=30\frac{m}{s}}{{v}_{35}}=-10\frac{m}{s}$ 

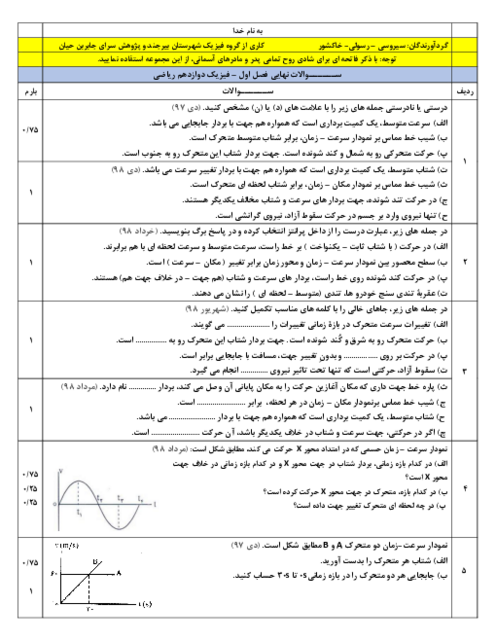
لحظات ${{t}_{1}}$ و ${{t}_{2}}$ كه متحرك تغيير جهت داده را به كمک تشابه مثلث‌ها می‌يابيم. داريم:

$_{\frac{{{t}_{2}}-15}{30}=\frac{35-{{t}_{2}}}{10}\Rightarrow {{t}_{2}}-15=105-3{{t}_{2}}\Rightarrow {{t}_{2}}=30s}^{\frac{{{t}_{1}}}{10}=\frac{10-{{t}_{1}}}{10}\Rightarrow 2{{t}_{1}}=10\Rightarrow {{t}_{1}}=5s}$ 

بنابراين نمودار سرعت – زمان متحرک مطابق شكل زير است.

با محاسبه‌ی مساحت‌ها كه برابر با جابه‌جايی در آن بازه است، داريم:

$_{\frac{1}{2}(10+30)5=100m,{{S}_{4}}=\frac{1}{2}\times 15\times 30=225m}^{{{S}_{1}}=\frac{1}{2}\times 5\times 10=25m,{{S}_{2}}=\frac{1}{2}\times 5\times 10=25m}$ 

${{s}_{av}}=\frac{l}{\Delta t}=\frac{\left| {{S}_{1}} \right|+\left| {{S}_{2}} \right|+\left| {{S}_{3}} \right|+\left| {{S}_{4}} \right|}{\Delta t}\Rightarrow {{s}_{av}}=\frac{25+25+100+225}{30}\Rightarrow {{s}_{av}}=\frac{25}{2}\frac{m}{s}$