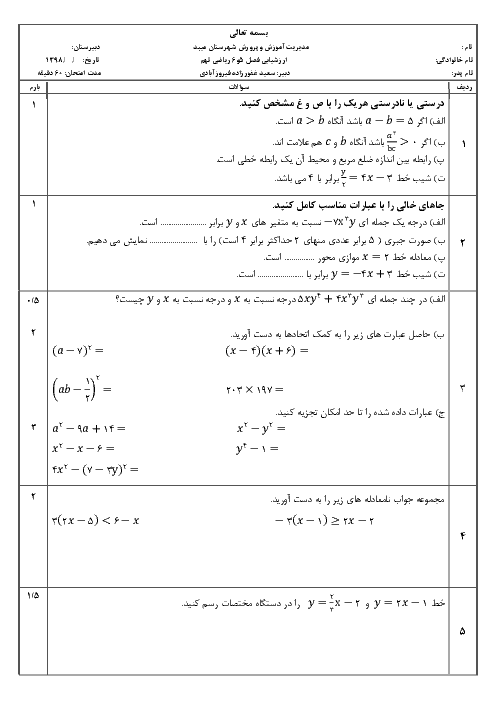
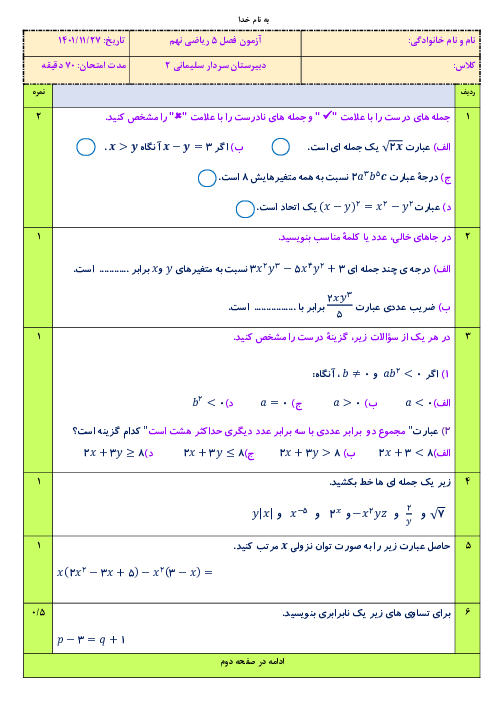
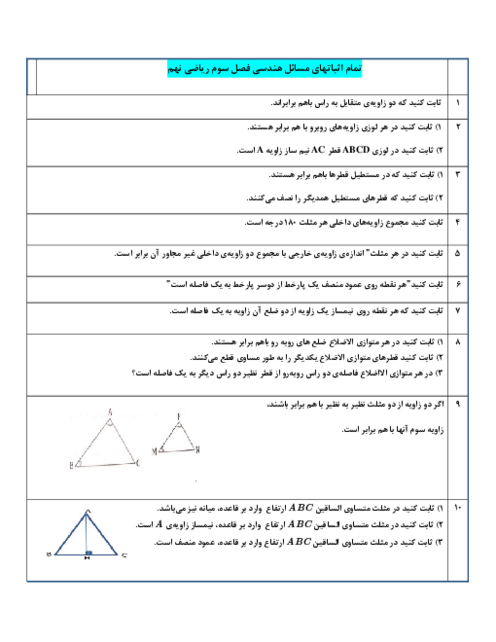
از برخورد خط 4x+5y=20 با محورهای مختصات، مثلث قائم‌الزاویه به وجود آمده است. نقطه‌ای به تصادف در این مثلث انتخاب می‌کنیم. احتمال آن که طول این نقطه از 3 واحد کمتر باشد، چقدر است؟
1 )
$ \frac{22}{25} $
$ \frac{21}{25} $
3 )
$ \frac{18}{25} $
4 )
$ \frac{4}{5} $
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...