** فصل 1: حرکت بر خط راست
فیزیک (3) ریاضی
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
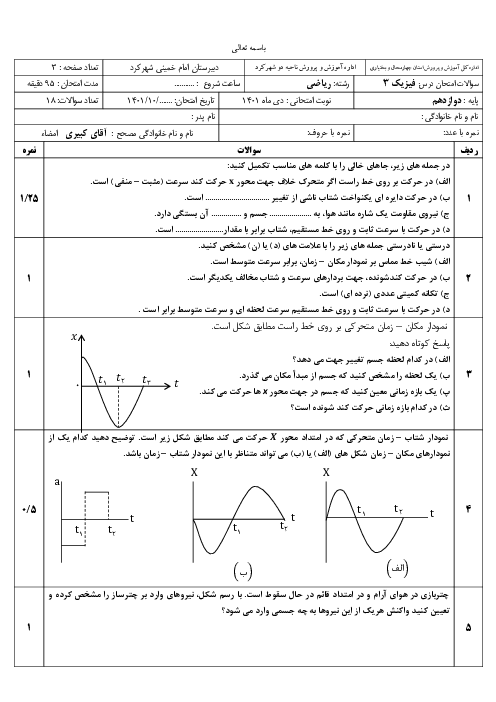
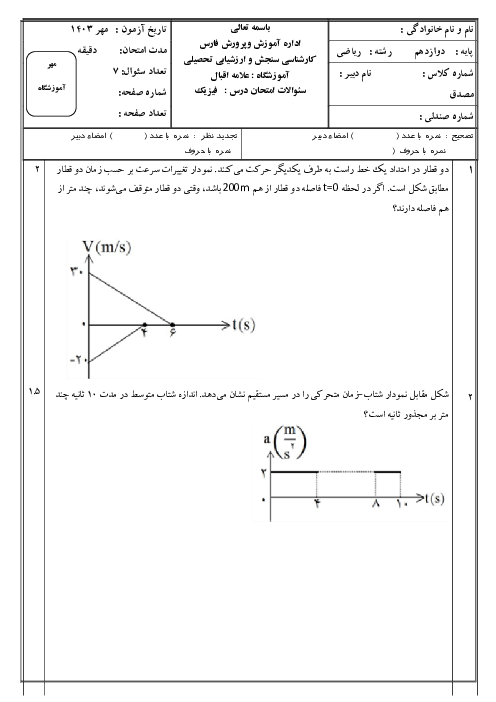
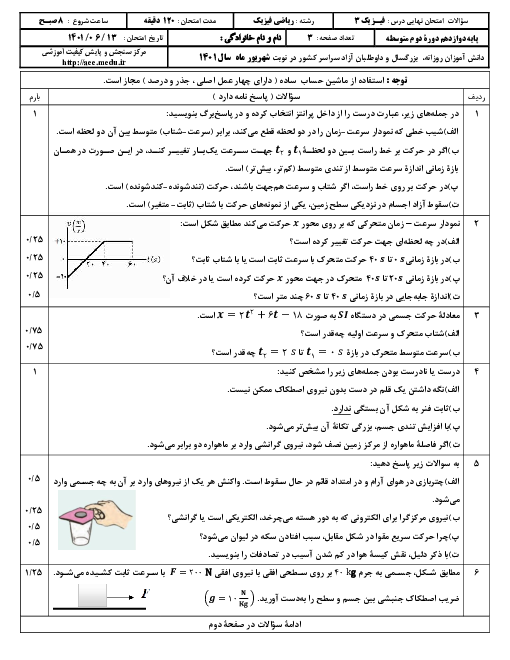
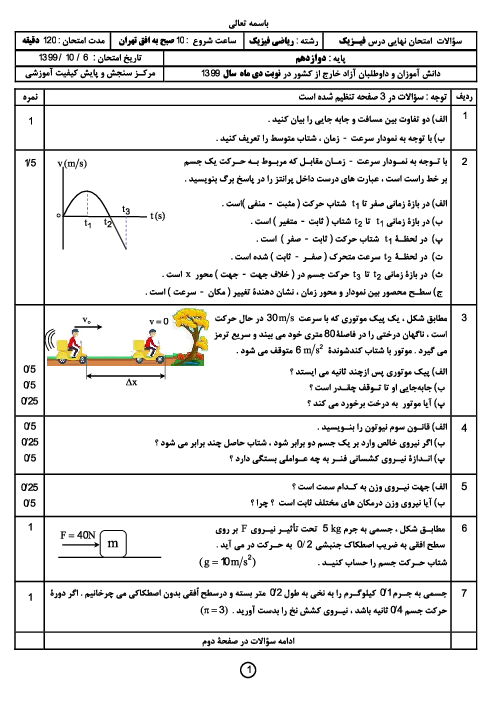
تندی لحظه‌ای متحرکی که در امتداد محور $x$ با شتاب ثابت حرکت می‌کند، در دو لحظه‌ی ${{t}_{1}}$ و ${{t}_{2}}$ به‌ترتیب ${{s}_{1}}$ و ${{s}_{2}}$ به‌ترتیب و سرعت لحظه‌ای آن ${{v}_{1}}$ و ${{v}_{2}}$ به‌ترتیب است. در این صورت کدام گزینه صحیح نیست؟ ($l$ مسافت پیموده شده و $\overrightarrow{d}$ بردار جابه‌جایی است.)
1 )
${{\overrightarrow{v}}_{av}}\frac{{{\overrightarrow{v}}_{2}}+\overrightarrow{{{v}_{1}}}}{2}$
${{\vec{v}}_{av}}\frac{{{\overrightarrow{s}}_{2}}+{{\overrightarrow{s}}_{1}}}{2}$
3 )
${{\overrightarrow{a}}_{av}}\frac{{{\overrightarrow{v}}_{2}}-{{\overrightarrow{v}}_{1}}}{{{t}_{2}}-{{t}_{1}}}$
4 )
$l\ge \left| \overrightarrow{d} \right|$
پاسخ تشریحی :
تحلیل ویدئویی تست
سعید احمدوند 
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...