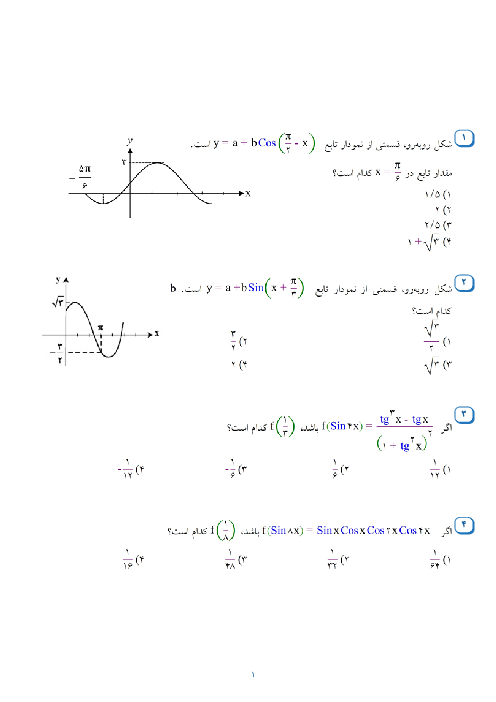
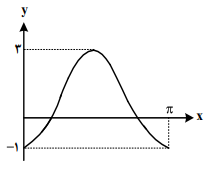
اگر شکل زیر، قسمتی از نمودار تابع $f(x) = a + b\sin (cx - \frac{{3\pi }}{4})\cos (cx - \frac{{3\pi }}{4})$ باشد، اختلاف صفرهای تابع $f$ در بازهٔ $\left[ {0,\pi } \right]$، کدام است؟
1 )
$\frac{\pi }{6}$
2 )
$\frac{\pi }{4}$
3 )
$\frac{\pi }{2}$
$\frac{{2\pi }}{3}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...