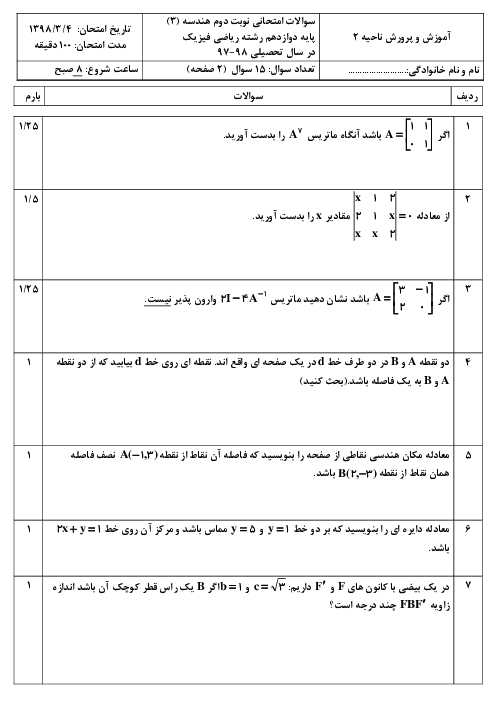
نکته: دترمینان ماتریس‌های $2\times 2$ به‌صورت روبه‌رو است:

$\left| \begin{matrix} \begin{matrix} a  \\ c  \\ \end{matrix} & \begin{matrix} b  \\ d  \\ \end{matrix}  \\ \end{matrix} \right|=ad-bc$

نکته: اگر $A=\left[ \begin{matrix} \begin{matrix} a  \\ c  \\ \end{matrix} & \begin{matrix} b  \\ d  \\ \end{matrix}  \\ \end{matrix} \right]$ در این‌صورت وارون ماتریس $A$ یعنی ${{A}^{-1}}$ از تساوی زیر به‌دست می‌آید.

${{A}^{-1}}=\frac{1}{\left| A \right|}.\left[ \begin{matrix} \begin{matrix} d  \\ -c  \\ \end{matrix} & \begin{matrix} -b  \\ a  \\ \end{matrix}  \\ \end{matrix} \right]$

با توجه به نکات داریم:

$A=\left[ \begin{matrix} \begin{matrix} 2  \\ 5  \\ \end{matrix} & \begin{matrix} m  \\ 3  \\ \end{matrix}  \\ \end{matrix} \right]\Rightarrow \left| A \right|=6-5m\Rightarrow {{A}^{-1}}=\frac{1}{6- 5m}\times \left[ \begin{matrix} \begin{matrix} 3  \\ -5  \\ \end{matrix} & \begin{matrix} -m  \\ 2  \\ \end{matrix}  \\ \end{matrix} \right]$

از طرفی مطابق فرض می‌توان نوشت:

$2A+{{A}^{-1}}=\left[ \begin{matrix} \begin{matrix} 7  \\ 5  \\ \end{matrix} & \begin{matrix} 1  \\ 8  \\ \end{matrix}  \\ \end{matrix} \right]\Rightarrow {{A}^{-1}}=\left[ \begin{matrix} \begin{matrix} 7  \\ 5  \\ \end{matrix} & \begin{matrix} 1  \\ 8  \\ \end{matrix}  \\ \end{matrix} \right]-2A=\left[ \begin{matrix} \begin{matrix} 7  \\ 5  \\ \end{matrix} & \begin{matrix} 1  \\ 8  \\ \end{matrix}  \\ \end{matrix} \right]-2\left[ \begin{matrix} \begin{matrix} 2  \\ 5  \\ \end{matrix} & \begin{matrix} m  \\ 3  \\ \end{matrix}  \\ \end{matrix} \right]=\left[ \begin{matrix} \begin{matrix} 3  \\ -5  \\ \end{matrix} & \begin{matrix} 1-2m  \\ 2  \\ \end{matrix}  \\ \end{matrix} \right]\Rightarrow $$\left[ \begin{matrix} \begin{matrix} \frac{3}{6-5m}  \\ \frac{-5}{6-5m}  \\ \end{matrix} & \begin{matrix} \frac{-m}{6-5m}  \\ \frac{2}{6-5m}  \\ \end{matrix}  \\ \end{matrix} \right]=\left[ \begin{matrix} \begin{matrix} 3  \\ -5  \\ \end{matrix} & \begin{matrix} 1-2m  \\ 2  \\ \end{matrix}  \\ \end{matrix} \right]$

$\left\{ \begin{matrix} \frac{3}{6-5m}=3\Rightarrow 6-5m=1\Rightarrow m=1  \\ \frac{-m}{6-5m}=1-2m\xrightarrow{m=1}\frac{-1}{1}=1-2\Rightarrow -1=-1\Rightarrow m=1\Rightarrow A\left[ \begin{matrix} \begin{matrix} 2  \\ 5  \\ \end{matrix} & \begin{matrix} 1  \\ 3  \\ \end{matrix}  \\ \end{matrix} \right]  \\ \end{matrix} \right.$

کافیست $A+I$ را تشکیل داده و دترمینان آن را محاسبه کنیم:

$A+I=\left[ \begin{matrix} \begin{matrix} 2  \\ 5  \\ \end{matrix} & \begin{matrix} 1  \\ 3  \\ \end{matrix}  \\ \end{matrix} \right]+\left[ \begin{matrix} \begin{matrix} 1  \\ 0  \\ \end{matrix} & \begin{matrix} 0  \\ 1  \\ \end{matrix}  \\ \end{matrix} \right]=\left[ \begin{matrix} \begin{matrix} 3  \\ 5  \\ \end{matrix} & \begin{matrix} 1  \\ 4  \\ \end{matrix}  \\ \end{matrix} \right]\Rightarrow \left| A+I \right|=12-5=7$