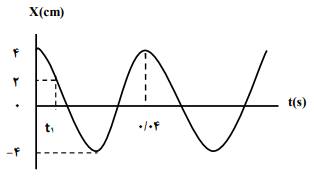
در شکل زیر نمودار مکان - زمان نوسانگر هماهنگ سادۀ جرم - فنری با دوره 0/04s و دامنه نوسان 4cm نشان داده شده است. اگر ثابت فنر این نوسانگر 60N/m باشد؛
الف) انرژی مکانیکی این نوسانگر چند ژول است؟
ب) مقدار ${t_1}$ چند ثانیه است؟ $(\cos \frac{\pi }{3} = \frac{1}{2})$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!