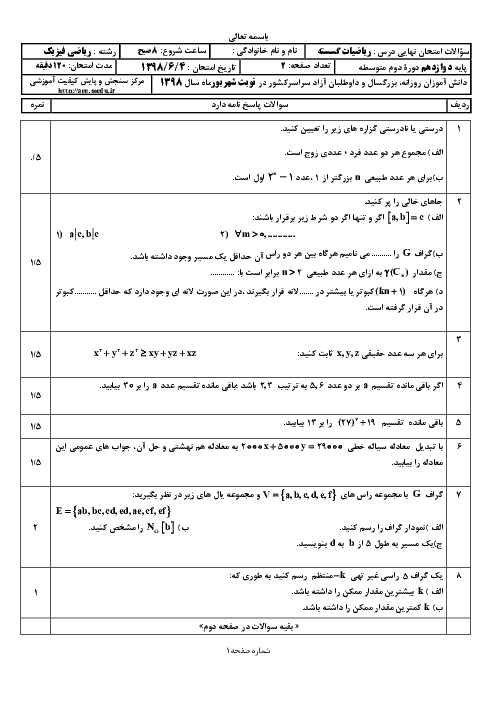
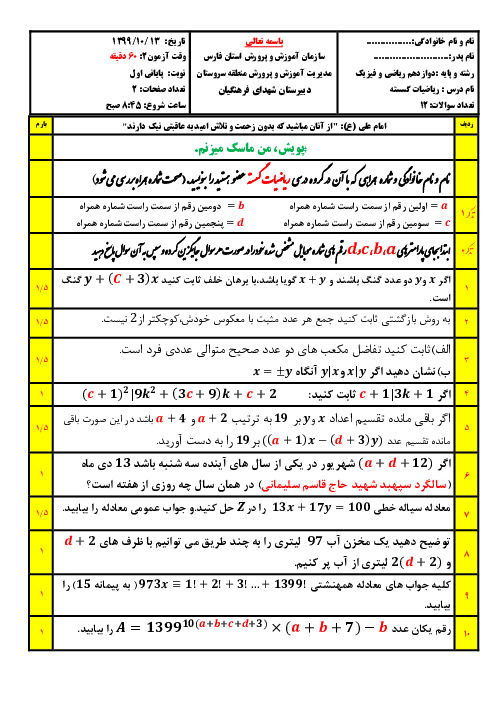
درس 2: بخشپذیری در اعداد صحیح
ریاضیات گسسته
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
دو عدد $a-1,{{a}^{2}}+a+3$ نسبت به هم اولاند. كدام گزاره همواره درست است؟