به ازای کدام مقادیر m معادلهٔ همواره فاقد ریشهٔ حقیقی است؟ | ریاضی و آمار (1) دهم شماره 245057 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت دوم سوالات امتحان نهایی هماهنگ نهم نمونه سوال گام به گام کاربرگ نوبت اول تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

آیا شما ربات هستید؟

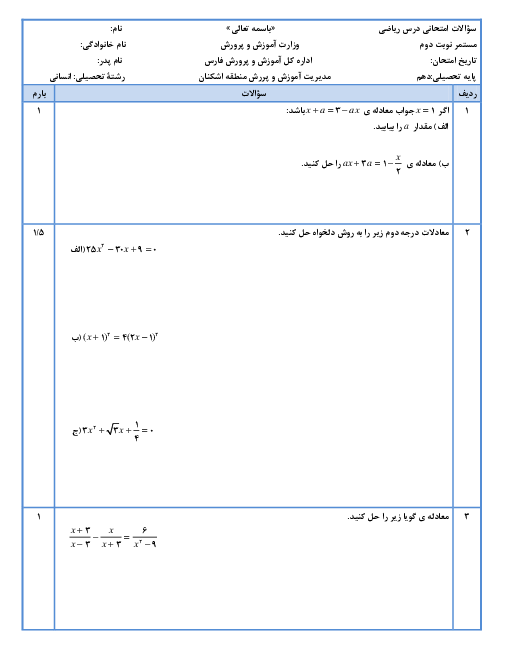
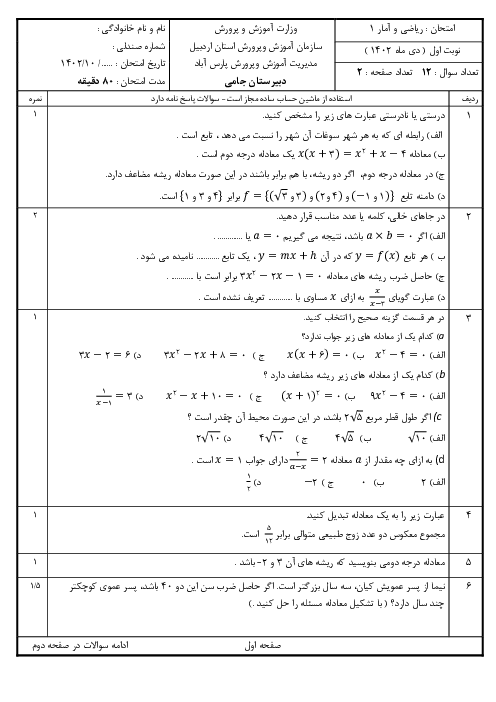
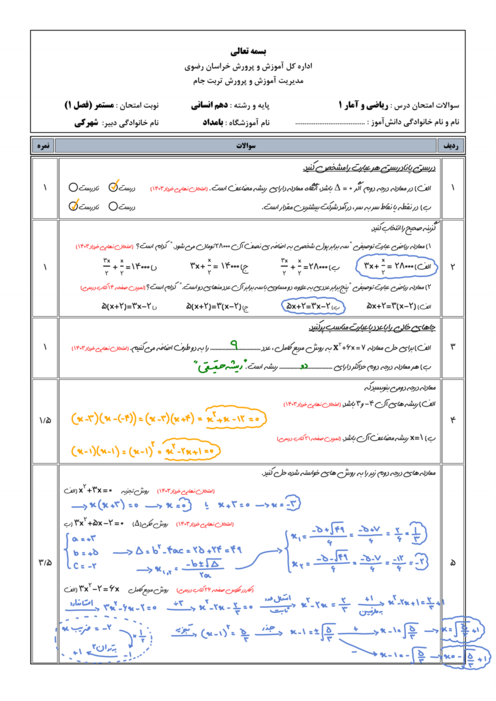
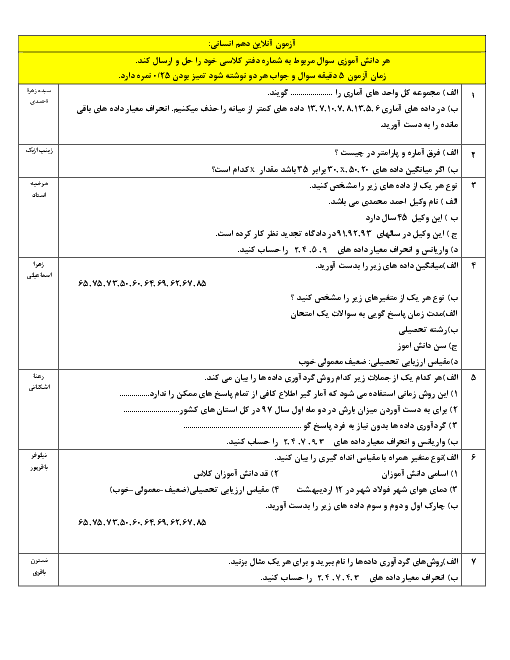
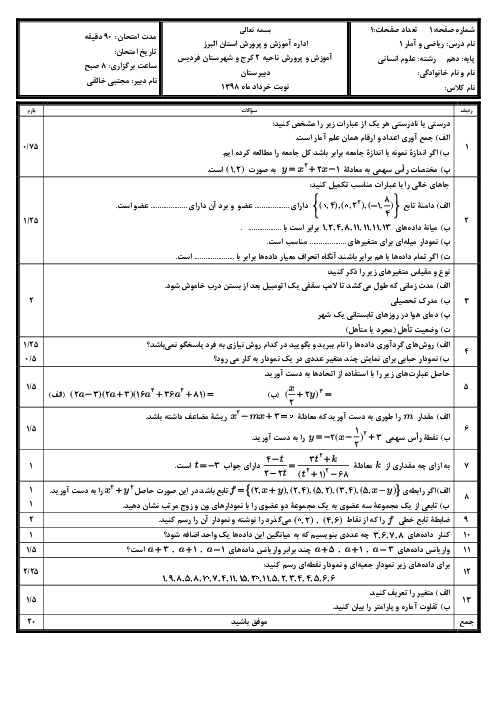
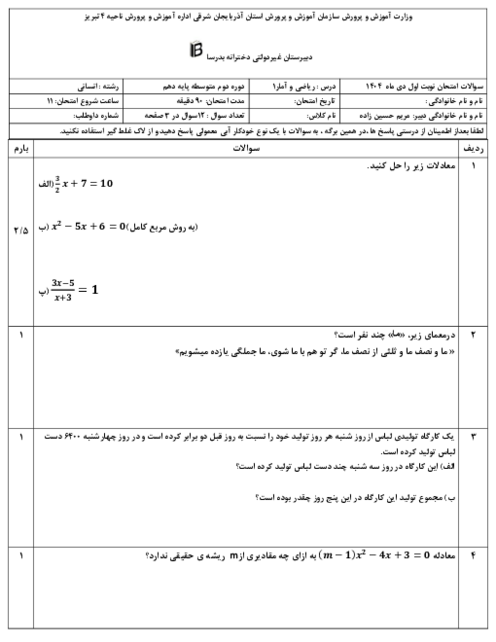
درس 2: حل معادلۀ درجۀ 2 و کاربردها ریاضی و آمار (1) دهم دوره دوم متوسطه- نظری ادبیات و علوم انسانی درسنامه آموزشی این مبحث

به ازای کدام مقادیر m معادلهٔ $x(mx - 2) = 6x + 2$ همواره فاقد ریشهٔ حقیقی است؟

1 )

$m \gt - 8$

2 )

$m \lt - 8$

3 )

$m \lt 8$

4 )

$m \gt 8$

نمایش پاسخ

ابتدا معادله را به‌صورت استاندارد مرتب می‌کنیم:

$x(mx - 2) = 6x + 2 \Rightarrow m{x^2} - 2x = 6x + 2$

$ \Rightarrow m{x^2} - 2x - 6x - 2 = 0$

$ \Rightarrow m{x^2} - 8x - 2 = 0 \to $ مقایسه با فرم استاندارد

$a{x^2} + bx + c = 0 \to $

$\eqalign{
& a = m \cr
& b = - 8 \cr
& c = - 2 \cr} $

$\Delta = {b^2} - 4ac \Rightarrow \Delta = {( - 8)^2} - 4 \times (m) \times ( - 2) = 64 + 8m$

برای این‌که معادلهٔ درجهٔ دوم فاقد ریشهٔ حقیقی باشد، می‌بایست $\Delta \lt 0$ باشد. در این‌صورت داریم:

$8m + 64 \lt 0 \Rightarrow 8m \lt - 64 \Rightarrow m \lt - \frac{{64}}{8} \Rightarrow m \lt - 8$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1402/07/7

علی شویعی نژاد

ویدیو دوره آموزشی، ریاضی و آمار (1) دهم دوره دوم متوسطه- نظری

مدرس: خدیجه اقدامی مقدم

مدت دوره: 5 ساعت (26 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

نمونه سوال امتحان ریاضی و آمار دهم دبیرستان هدف | حل معادله درجه 2 و کاربردها

4 صفحه

نمونه سوال امتحان ریاضی و آمار دهم دبیرستان هدف | حل معادله درجه 2 و کاربردها

مجید سلطان آبادی

آزمون نوبت دوم ریاضی و آمار (1) دهم انسانی دبیرستان اندیشه |‌ خرداد 1396

2 صفحه

آزمون نوبت دوم ریاضی و آمار (1) دهم انسانی دبیرستان اندیشه |‌ خرداد 1396

فاروق بختیاری نژاد

گام به گام ریاضی و آمار (1) پایه دهم رشته انسانی و معارف | فصل 4: داده های آماری

14 صفحه

گام به گام ریاضی و آمار (1) پایه دهم رشته انسانی و معارف | فصل 4: داده…

گام به گام دهم

تکلیف و تمرین ریاضی و آمار (1) دهم انسانی | فصل 2: تابع

39 صفحه

تکلیف و تمرین ریاضی و آمار (1) دهم انسانی | فصل 2: تابع

یداله سالمی

امتحان ریاضی و آمار (1) دهم دبیرستان شهید بهشتی | ترم دوم خرداد 1402

4 صفحه

امتحان ریاضی و آمار (1) دهم دبیرستان شهید بهشتی | ترم دوم خرداد 1402

جواد راستگویان

امتحان ترم دوم ریاضی و آمار (1) دهم دبیرستان حضرت زهرا | خرداد 1401

6 صفحه

امتحان ترم دوم ریاضی و آمار (1) دهم دبیرستان حضرت زهرا | خرداد 1401

فاطمه بوربور

خلاصه درس و نمونه سوالات امتحانی ریاضی و آمار (1) دهم انسانی

104 صفحه

خلاصه درس و نمونه سوالات امتحانی ریاضی و آمار (1) دهم انسانی

پریا عالی

آزمون نوبت دوم ریاضی و آمار دهم انسانی دبیرستان امام خمینی | خرداد 1398 + جواب

2 صفحه

آزمون نوبت دوم ریاضی و آمار دهم انسانی دبیرستان امام خمینی | خرداد 1398…

اسماعیل ادبی فیروزجایی

آزمونک ریاضی و آمار دهم دبیرستان دکتر حسابی | چند اتحاد جبری و کاربردها

1 صفحه

آزمونک ریاضی و آمار دهم دبیرستان دکتر حسابی | چند اتحاد جبری و کاربردها

محمد ایزدی

امتحان نوبت اول رياضی و آمار (1) دهم رشته ادبیات و علوم انسانی دبیرستان دخترانۀ شاهد یزد | دی 96

3 صفحه

امتحان نوبت اول رياضی و آمار (1) دهم رشته ادبیات و علوم انسانی دبیرستان…

نرگس نوفرد

موارد بیشتر

موارد بیشتر

ارسال فایل

حقوق یک فن‌ورز در این کارخانه ماهیانه چقدر است؟

در معادله 4x(x-1)=3،اختلاف دو ریشه کدام است؟

سن بیتا و برادرش در مسئله سن

موارد بیشتر

ارسال پرسش

موارد بیشتر