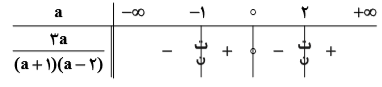
اگر $\frac{\pi }{2} \gt \alpha \gt \beta \gt -\frac{\pi }{2}$، $\tan \alpha =\frac{1}{a+1}$ و $\tan \beta =\frac{-2}{a-2}$، دقیق ترین محدودهٔ $a$ کدام است؟
1 )
$(-2,+\infty )$
$(-1,0)\bigcup (2,+\infty )$
3 )
$(-\infty ,-1)\bigcup (0,1)$
4 )
$(-\infty ,-2)\bigcup (2,+\infty )$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...