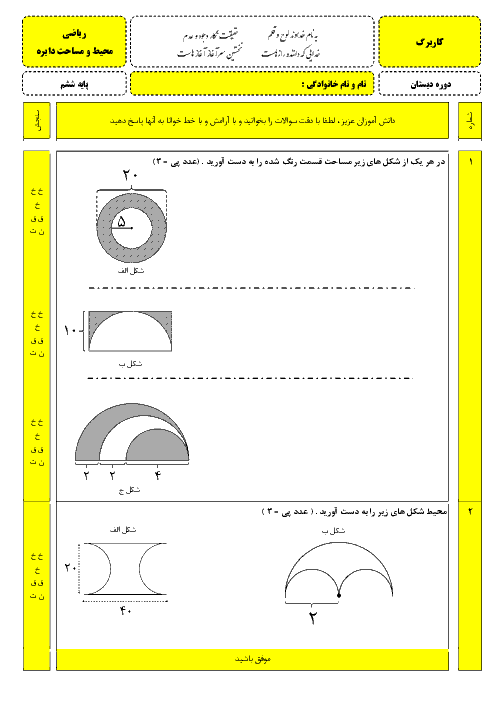
اگر قرینه‌ی چهار ضلعی (آ ب ج د) را نسبت به محور افقی رسم کنیم و قرینه‌ی نقطه‌ی (آ) را (م) و قرینه‌ی نقطه‌ی (ج) را (س) بنامیم. مختصات نقاط (م) و (س) چقدر است؟
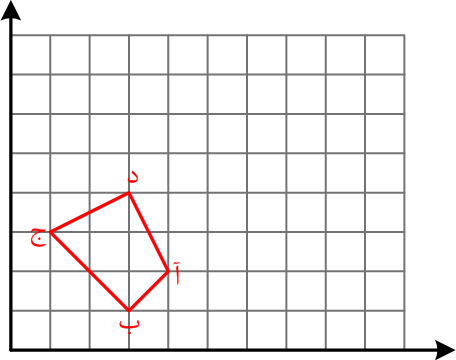
1 )
$\left[ \begin{matrix} 1 \\ -3 \\ \end{matrix} \right]$ م $\left[ \begin{matrix} 4 \\ 2 \\ \end{matrix} \right]$ س
$\left[ \begin{matrix} 4 \\ -2 \\ \end{matrix} \right]$ م $\left[ \begin{matrix} 1 \\ -3 \\ \end{matrix} \right]$ س
3 )
$\left[ \begin{matrix} 3 \\ 1 \\ \end{matrix} \right]$ م $\left[ \begin{matrix} 4 \\ -2 \\ \end{matrix} \right]$ س
4 )
$\left[ \begin{matrix} 1 \\ -3 \\ \end{matrix} \right]$ م $\left[ \begin{matrix} 4 \\ -2 \\ \end{matrix} \right]$ س
پاسخ تشریحی :
تحلیل ویدئویی تست
ریحانه احمدی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...