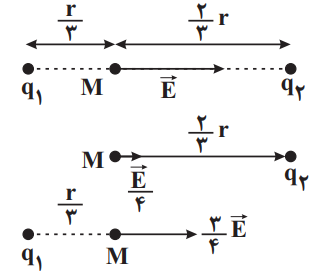
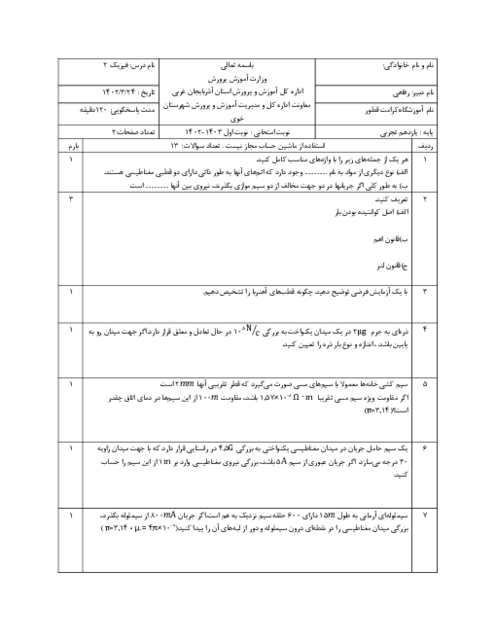
با حضور دو بار، میدان الکتریکی برایند در نقطهٔ M برابر $\overrightarrow{E}$ است و با حذف ${{q}_{1}}$ میدان الکتریکی تنها حاصل از بار ${{q}_{2}}$ خواهد بود که برابر $\frac{\overrightarrow{E}}{4}$ است. پس داریم:
با فرض0>${{q}_{2}}$

$\left. \begin{matrix}
   {{\overrightarrow{E}}_{1}}+{{\overrightarrow{E}}_{2}}=\overrightarrow{E}  \\
   {{\overrightarrow{E}}_{2}}=\frac{\overrightarrow{E}}{4}\,\,\,\,\,\,\,\,\,\,  \\
\end{matrix} \right\}{{\overrightarrow{E}}_{1}}=\frac{3\overrightarrow{E}}{4}$

    $E=\frac{k\left| q \right|}{{{r}^{2}}}\Rightarrow \left| \frac{{{E}_{2}}}{{{E}_{1}}} \right|=\left| \frac{{{q}_{2}}}{{{q}_{1}}} \right|\times {{(\frac{{{r}_{1}}}{{{r}_{2}}})}^{2}}\Rightarrow \left| \frac{\frac{E}{4}}{\frac{3E}{4}} \right|=\left| \frac{{{q}_{2}}}{{{q}_{1}}} \right|\times {{(\frac{\frac{r}{3}}{\frac{2r}{3}})}^{2}}\Rightarrow \frac{1}{3}=\left| \frac{{{q}_{2}}}{{{q}_{1}}} \right|\times \frac{1}{4}\Rightarrow \left| \frac{{{q}_{2}}}{{{q}_{1}}} \right|=\frac{4}{3}$

حال با توجه به این‌که ${{\overrightarrow{E}}_{1}}=\frac{3\overrightarrow{E}}{4}$ و ${{\overrightarrow{E}}_{2}}=\frac{\overrightarrow{E}}{4}$ میدان‌ها در نقطهٔ M هم‌جهت‌اند، پس می‌توان نتیجه گرفت که دو بار مختلف العلامت‌اند پس:

$\frac{{{q}_{2}}}{{{q}_{1}}}=-\frac{4}{3}$