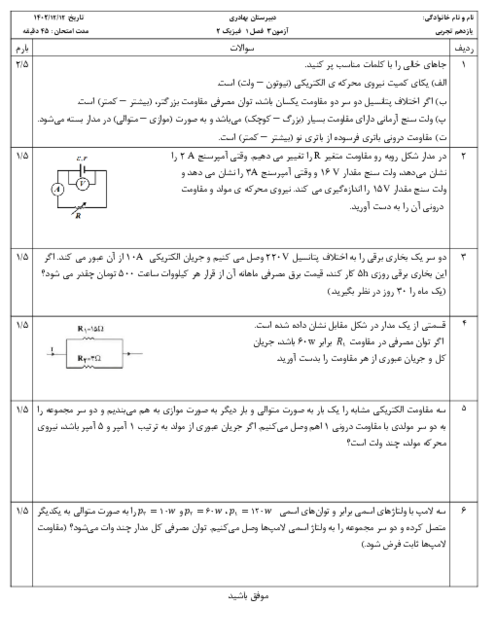
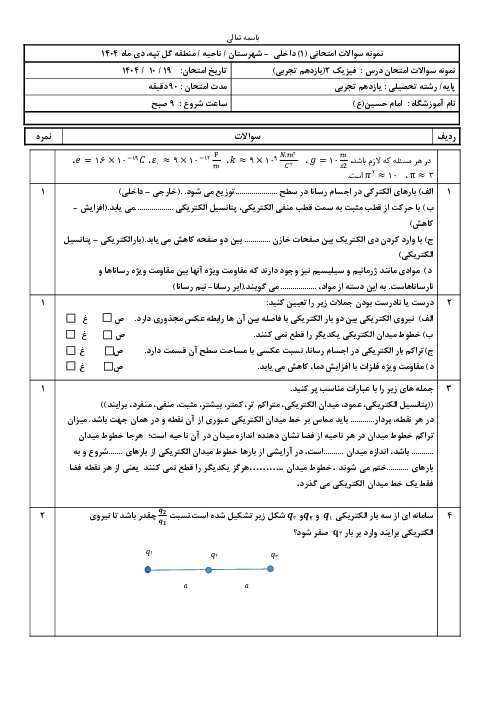
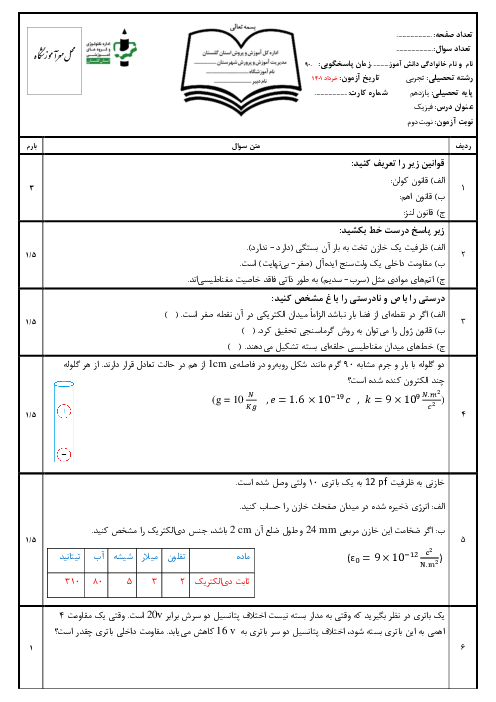
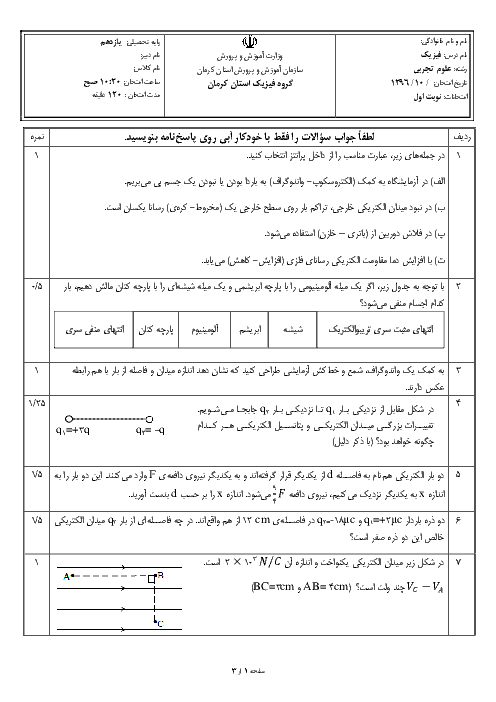
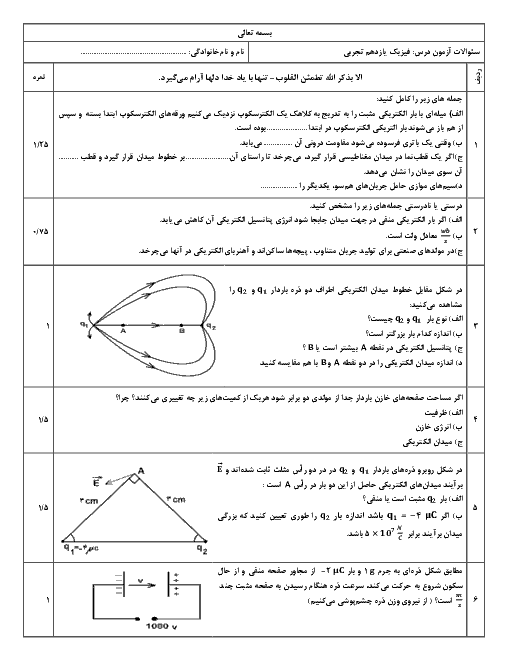
از آنجایی که نیروی واردبه بار ${{q}_{2}}$ از طرف ${{q}_{1}}$ به سمت چپ و به صورت جاذبه است، پس علامت بار ${{q}_{1}}$ منفی می‌باشد. حال مقدار آن را محاسبه می‌کنیم:

$F=k\frac{\left| {{q}_{1}} \right|\left| {{q}_{2}} \right|}{{{r}^{2}}}\Rightarrow 50=9\times {{10}^{9}}\times \frac{\left| {{q}_{1}} \right|\times 1\times {{10}^{-6}}}{{{(3\times {{10}^{-2}})}^{2}}}\Rightarrow \left| {{q}_{1}} \right|=5\mu C\xrightarrow[{}]{{{q}_{1\lt0}}}{{q}_{1}}=5\mu C$

در نقطهٔ O داریم:

$E=k\frac{\left| q \right|}{{{r}^{2}}}\Rightarrow \left\{ \begin{matrix}
   {{E}_{1}}=9\times {{10}^{9}}\times \frac{5\times {{10}^{-6}}}{{{(3\times {{10}^{-2}})}^{2}}}=5\times {{10}^{7}}\frac{N}{C}\Rightarrow {{\overrightarrow{E}}_{1}}=5\times {{10}^{7}}\frac{N}{C}\overrightarrow{i}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,  \\
   {{E}_{2}}=9\times {{10}^{9}}\times \frac{1\times {{10}^{-6}}}{{{(6\times {{10}^{-2}})}^{2}}}=2/5\times {{10}^{6}}\frac{N}{C}\Rightarrow {{\overrightarrow{E}}_{2}}=-2/5\times {{10}^{6}}\frac{N}{C}\overrightarrow{i}  \\
\end{matrix} \right.$

با توجه به تصویر
با توجه به خلاف جهت هم بودن میدان‌های ناشی از ${{q}_{1}}$ و ${{q}_{2}}$، در نقطـهٔ O، داریم:

${{E}_{O}}={{\overrightarrow{E}}_{1}}+{{\overrightarrow{E}}_{2}}=50\times {{10}^{6}}\overrightarrow{i}-2/5\times {{10}^{-6}}\overrightarrow{i}=47/5\times {{10}^{6}}\overrightarrow{i}(\frac{N}{C})$