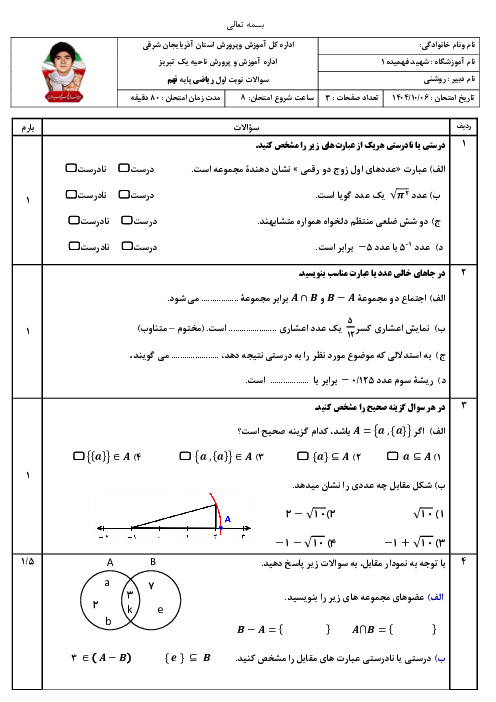
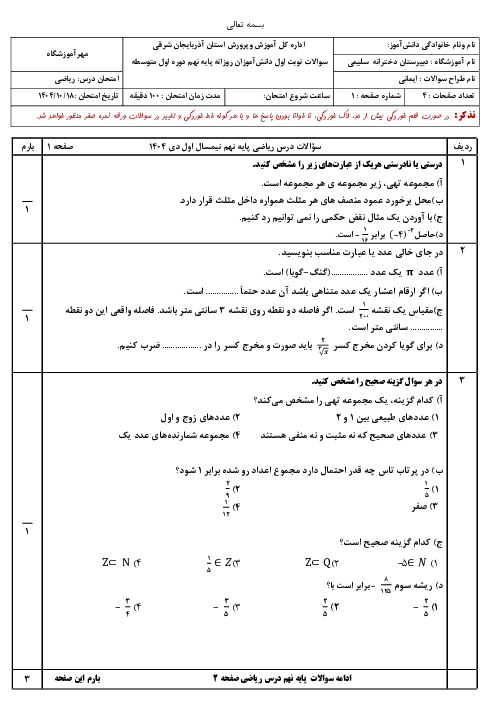
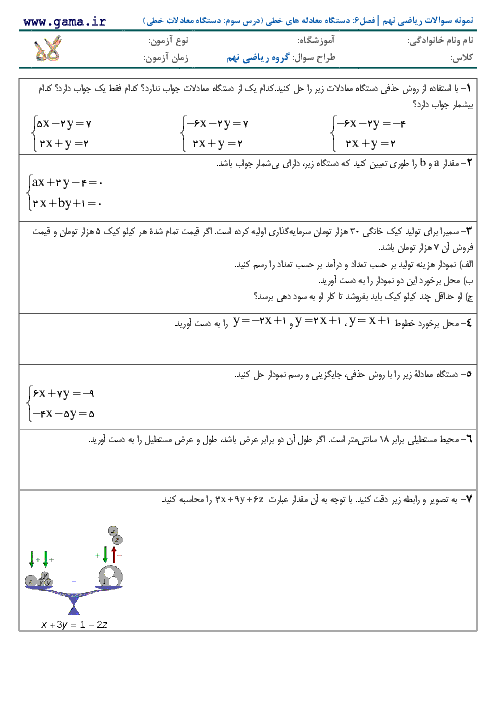
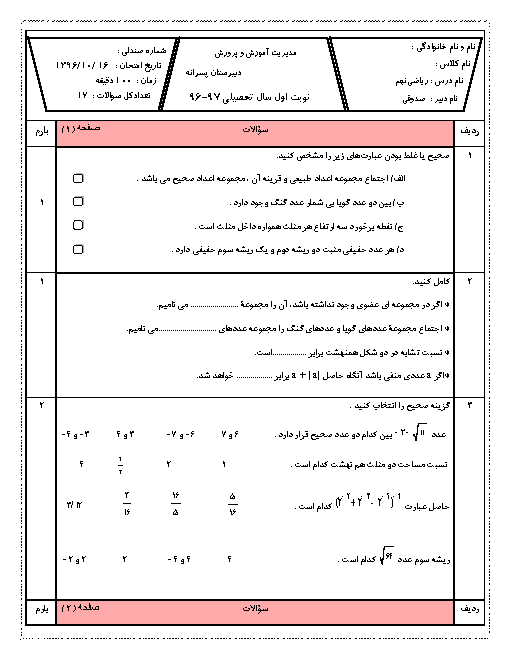
از آنجاکه $M - N = \left\{ 3 \right\}$، می‌توان نتیجه گرفت:

1) $ - 7 \notin M$

2) $3 \in M$

3) $3 \notin N$

$M \ne \emptyset ,M \subseteq \left\{ {3,0,6} \right\}$

$M - \left\{ 3 \right\} \subseteq N,N \subseteq \left\{ {0,6} \right\}$

حالا حالت‌های ممکن برای مجموعهٔ M را نوشته و در هر حالت Nهای قابل قبول را نیز می‌یابیم.

حالت اول برای M: $M = \left\{ 3 \right\}$

های قابل قبولN: $\left\{ {\begin{array}{*{20}{c}}
  {N = \left\{ {} \right\} \to (\{ 3\} ,\emptyset )} \\ 
  {N = \left\{ 0 \right\} \to (\{ 3\} ,\{ 0\} )} \\ 
  {N = \{ 6\}  \to (\{ 3\} ,\{ 6\} )} \\ 
  {N = \{ 0,6\}  \to (\{ 3\} ,\{ 0,6\} )} 
\end{array}} \right.$

حالت دوم برای M: $M = \{ 3,0\} $

 های قابل‌قبولN: $\left\{ {\begin{array}{*{20}{c}}
  {N = \{ 0,6\}  \to (\{ 0,3\} ,\{ 0,6\} )} \\ 
  {N = \{ 0\}  \to (\{ 0,3\} ,\{ 0\} )} 
\end{array}} \right.$

حالت سوم برای M: $M = \{ 3,6\} $

های قابل قبولN: $\left\{ {\begin{array}{*{20}{c}}
  {N = \{ 6\}  \to (\{ 3,6\} ,\{ 6\} )} \\ 
  {N = \{ 0,6\}  \to (\{ 3,6\} ,\{ 0,6\} )} 
\end{array}} \right.$

حالت چهارم برای M: $M = \{ 3,0,6\} $

های قابل قبولN: $N = \{ 0,6\}  \to (\{ 3,0,6\} ,\{ 0,6\} )$