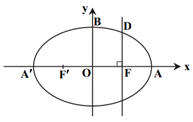
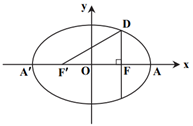
نكته: مجموع فاصلههای هر نقطه روی بيضی از دو كانون، برابر با مقدار ثابت 2a است.
چون $OF=AF=2$، پس مختصات نقطههای $A$، $F$ و ${F}'$ بهصورت مقابل است:
$F(2,0),A(4,0),{F}'(-2,0)$
$OA=4\Rightarrow a=4$
مختصات نقطۀ $D$ بهصورت $D(2,b)$ است. داريم:
$DF=b,D{F}'=\sqrt{{{(2+2)}^{2}}+{{(b-0)}^{2}}}=\sqrt{16+{{b}^{2}}}$
$DF+D{F}'=2a\Rightarrow b+\sqrt{16+{{b}^{2}}}=8\Rightarrow \sqrt{16+{{b}^{2}}}=8-b$
$\Rightarrow 16+{{b}^{2}}=64-16b+{{b}^{2}}\Rightarrow 16b=48\Rightarrow b=3\Rightarrow D(2,3)$
بنابراین طول پارهخط $AD$ برابر است با:
$AD=\sqrt{{{(4-2)}^{2}}+{{(0-3)}^{2}}}=\sqrt{4+9}=\sqrt{13}$