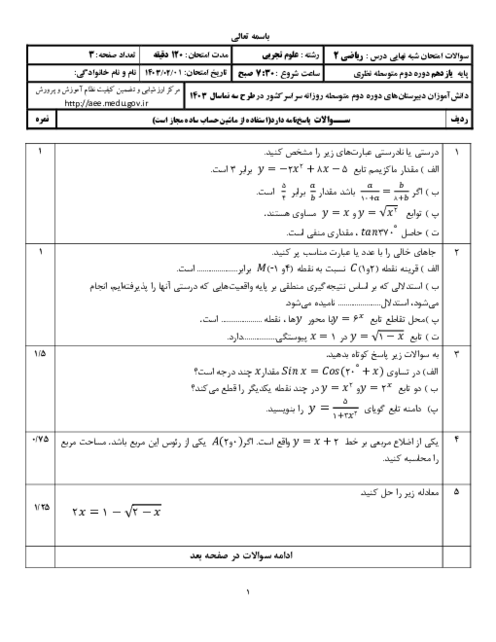
میانگین گروه اول داده‌ها عبارت است از؛

$\begin{align}  & \bar{x}=\frac{{{x}_{1}}-1+{{x}_{2}}-2+...+{{x}_{n}}-n}{n} \\  & \Rightarrow \bar{x}=\frac{{{x}_{1}}+{{x}_{2}}+...+{{x}_{n}}-(1+2+...+n)}{n} \\  & \Rightarrow \bar{x}=\frac{{{x}_{1}}+{{x}_{2}}+...+{{x}_{n}}-\frac{n(n+1)}{2}}{n} \\  & \Rightarrow \bar{x}=\frac{{{x}_{1}}+{{x}_{2}}+...+{{x}_{n}}}{n}-\frac{n+1}{2} \\  & \Rightarrow \frac{{{x}_{1}}+{{x}_{2}}+...+{{x}_{n}}}{n}=\bar{x}+\frac{n+1}{2}(1) \\ \end{align}$

میانگین گروه دوم داده‌ها عبارت است از؛

$ \begin{align}  & \overline{Y}=\frac{{{x}_{1}}+1+{{x}_{2}}+2+...+{{x}_{n}}+n}{n} \\  & \Rightarrow \overline{Y}=\frac{{{x}_{1}}+{{x}_{2}}+...+{{x}_{n}}+(1+2+...+n)}{n} \\  & \Rightarrow \overline{Y}=\frac{{{x}_{1}}+{{x}_{2}}+...+{{x}_{n}}+\frac{n(n+1)}{2}}{n} \\  & \Rightarrow \overline{Y}=\frac{{{x}_{1}}+{{x}_{2}}+...+{{x}_{n}}}{n}+\frac{n+1}{2} \\  & \xrightarrow{(1)}\overline{Y}=\overline{x}+\frac{n+1}{2}+\frac{n+1}{2}\to \overline{Y}=\overline{x}+n+1 \\ \end{align} $