در شکل زیر، نمودار مکان - زمان متحرکی در حرکت یک بعدی با شتاب ثابت دیده می‌شود. معادله‌ی حرکت مربوط به این متحرک در کدام است؟ | فیزیک (3) ریاضی دوازدهم شماره 74306

گاما رو نصب کن!

درحال دریافت اطلاعات ...

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت دوم سوالات امتحان نهایی هماهنگ نهم نمونه سوال گام به گام کاربرگ نوبت اول تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

این مدرسه منحل یا غیرفعال شده است. لطفا از لیست مدارس مشابه استفاده کنید.

قسمت 1: شناخت حرکت فیزیک (3) ریاضی دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

در شکل زیر، نمودار مکان - زمان متحرکی در حرکت یک بعدی با شتاب ثابت دیده می‌شود. معادله‌ی حرکت مربوط به این متحرک در $SI$ کدام است؟

1 )

$x={{t}^{2}}-12t+36$

2 )

$x=2{{t}^{2}}-12t+18$

3 )

$x=\frac{1}{2}{{t}^{2}}-12t+36$

4 )

$x=\frac{1}{2}{{t}^{2}}-12t+18$

نمایش پاسخ

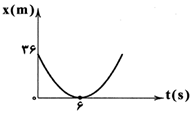
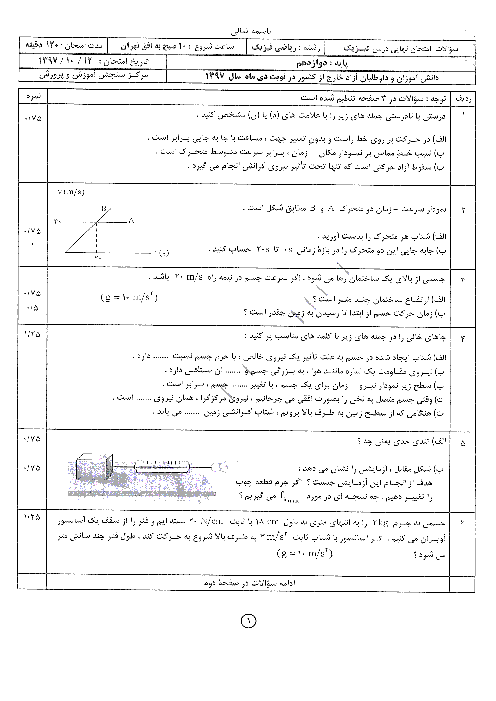
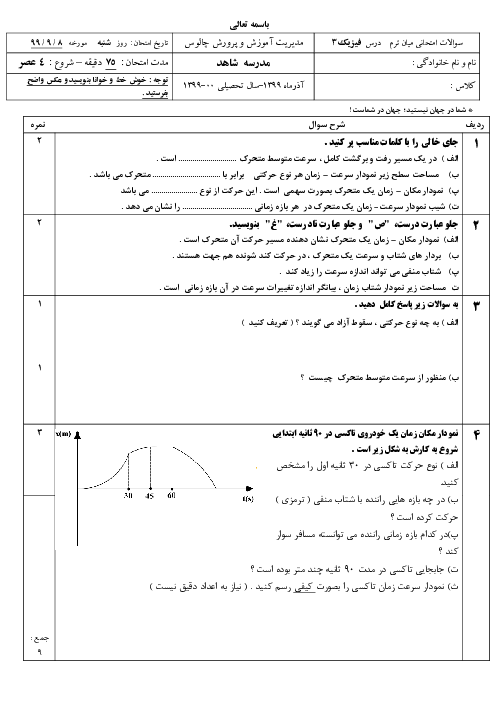
نمودار، سهمی است. پس با توجه به متقارن بودن نمودار در لحظه‌ی $t=12s$ متحرک دوباره به مکان 36 متری مبدأ می‌رسد. حال با استفاده از معادله‌ی مکان - زمان شتاب متحرک را محاسبه می‌کنیم.

$\Delta x=\frac{1}{2}a{{t}^{2}}+{{v}_{{}^\circ }}t\Rightarrow -36=\frac{1}{2}a\times {{6}^{2}}+6{{v}_{{}^\circ }}\Rightarrow -36=18a+6{{v}_{{}^\circ }}$ (1)

در لحظه‌ی $t=6s$ سرعت متحرک صفر است:

$v=at+{{v}_{{}^\circ }}\Rightarrow 0=6a+{{v}_{{}^\circ }}\Rightarrow {{v}_{{}^\circ }}=-6a$ (2)

از (1) و (2) نتیجه می‌شود که $a=2\frac{m}{{{s}^{2}}}$ و ${{v}_{{}^\circ }}=-12\frac{m}{s}$.

مکان اولیه‌ی متحرک در 36 متری مبدأ است.

$x=\frac{1}{2}\times 2{{t}^{2}}-12t+36\Rightarrow x={{t}^{2}}-12t+36$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده