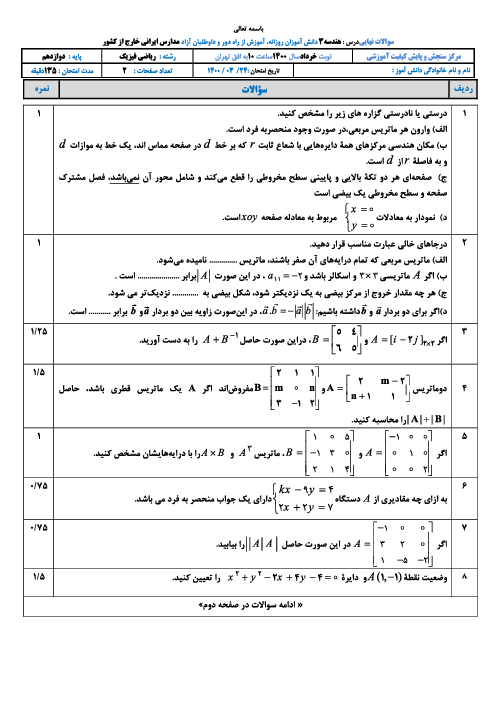
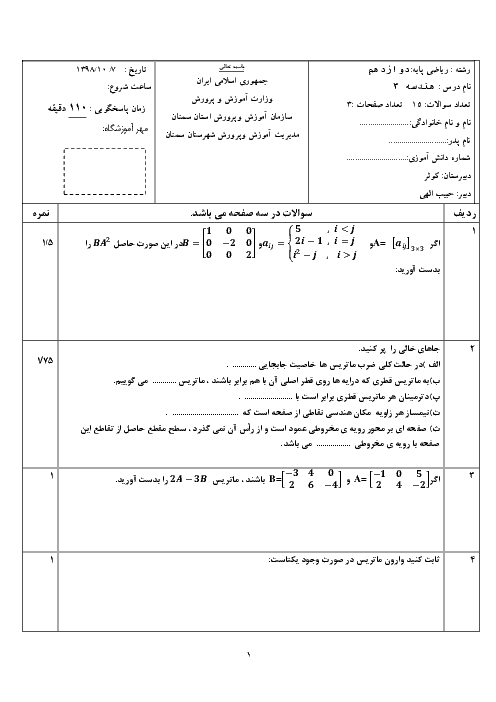
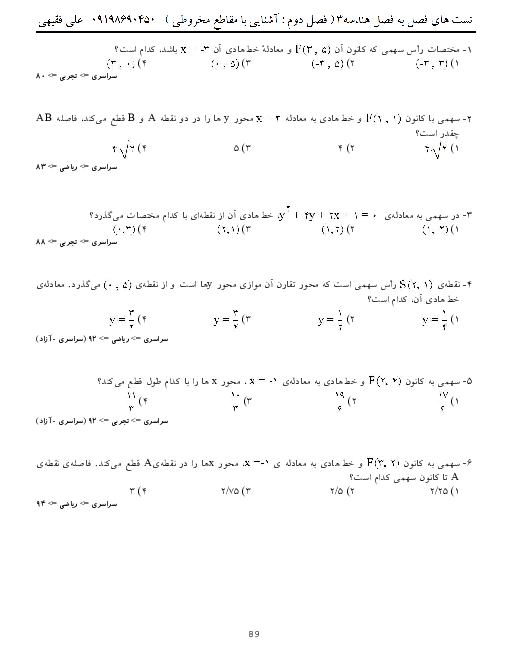
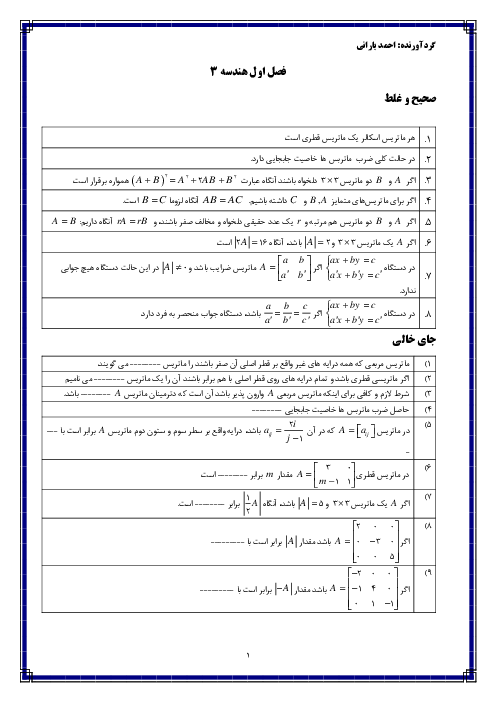
در شکل زیر خط $d$ در نقطهٔ $B$ بر بیضی مماس است. از کانون $F$ عمودی بر $BF$ رسم کرده‌ایم تا خط $d$ را در نقطهٔ $C$ قطع کند. سپس از $C$ عمودی بر امتداد قطر بزرگ رسم کرده‌ایم. اگر در این بیضی $b=c$ طول $AD$ کدام است؟
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...