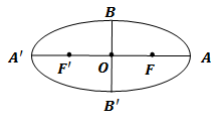
در بیضی روبهرو: $OF = OF' = c\,,\,OB = OB' = b\,,\,OA = OA' = a$ ثابت کنید: ${b^2} + {c^2} = {a^2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!

گاما رو نصب کن!
جستجو
پربازدیدها: #{{ tag.title }}
به پاس اعتمادی که به گاما داشتی، ما اشتراک ویژهای رو برات فعال کردیم تا بدون هیچ نگرانی از محدودیت زمانی، از سرویسهای ویژه گاما استفاده کنی.
اگه به اطلاعات بیشتری نیاز داری راهنمای تغییرات جدید رو ببین.
از همراهیت با گاما سپاسگزاریم.
با تقدیم احترام
با سپاس! گزارش شما ثبت شد.