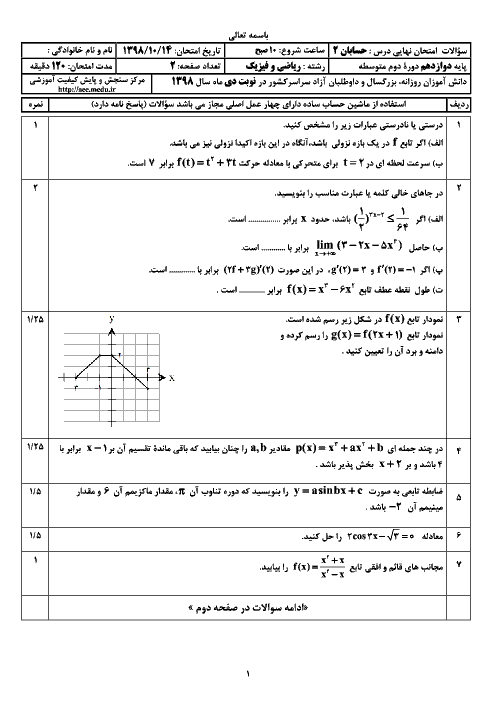
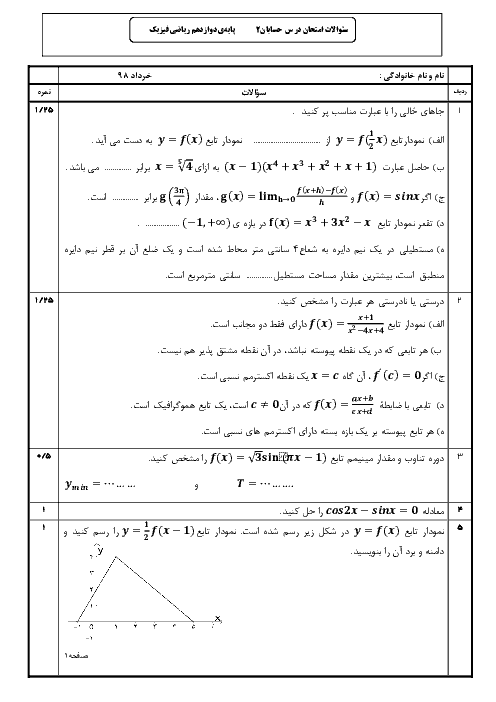
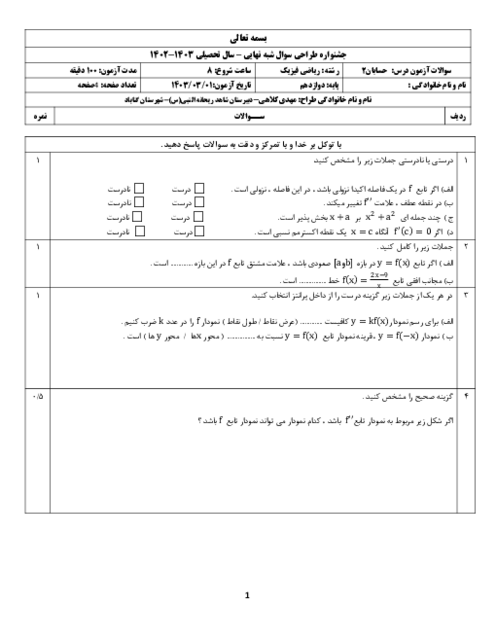
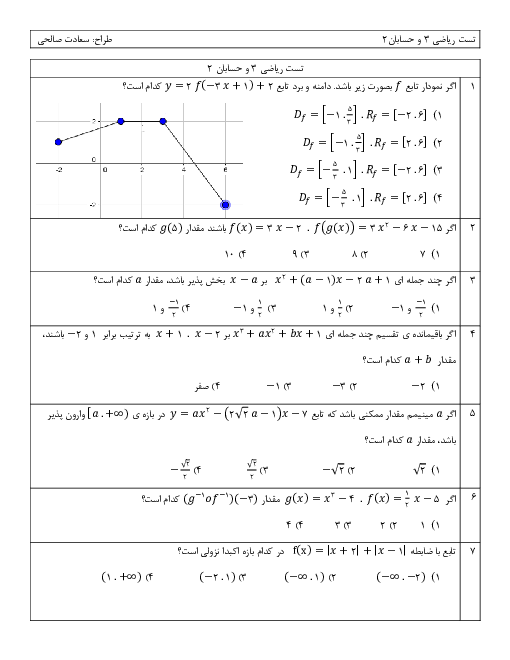
درس 2: جهت تقعر نمودار یک تابع و نقطۀ عطف آن
حسابان (2)
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
در تابع با ضابطهٔ $y={{({{x}^{2}}-1)}^{3}}$ نقاط بحرانی بهترتیب از چپ به راست چگونهاند؟
1 )
عطف- ماکزیمم نسبی- عطف
2 )
ماکزیمم نسبی- عطف- ماکزیمم نسبی
عطف- مینیمم نسبی- عطف
4 )
مینیمم نسبی- عطف- مینیمم نسبی