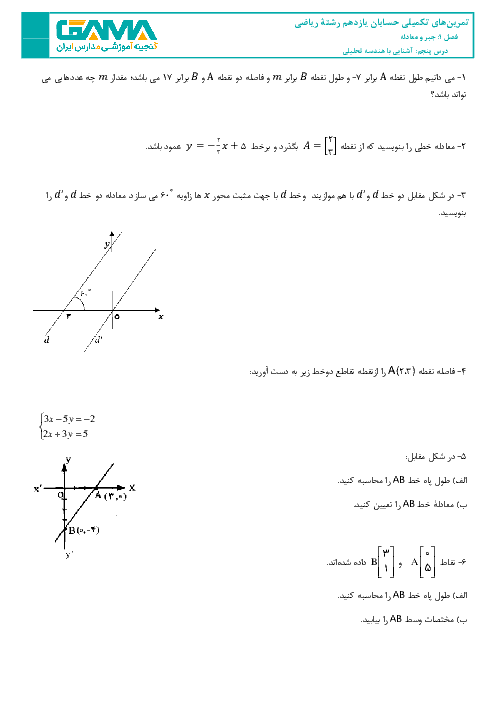
اگر f+g و f-g هر دو در نقطۀ $x_0$ پیوسته باشند، آنگاه کدام بیان درست است؟
1 )
الزاماً تابع $\frac{f}{g}$ در $x_0$ پیوسته است.
2 )
$f \times g$ ممکن است در $x_0$ پیوسته نباشد.
3 )
f یا g ممکن است در $x_0$ پیوسته نباشد.
الزاماً f و g هر دو در $x_0$ پیوسته‌اند.
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...