قسمت 4: نیروی مغناطیسی وارد بر سیم حامل جریان
فیزیک (2)
یازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
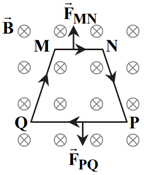
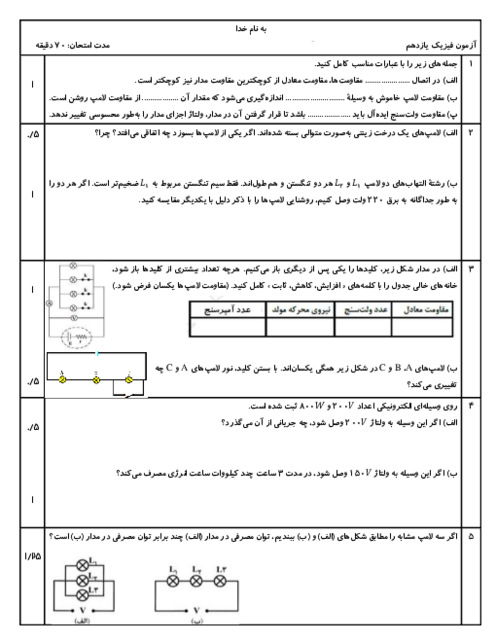
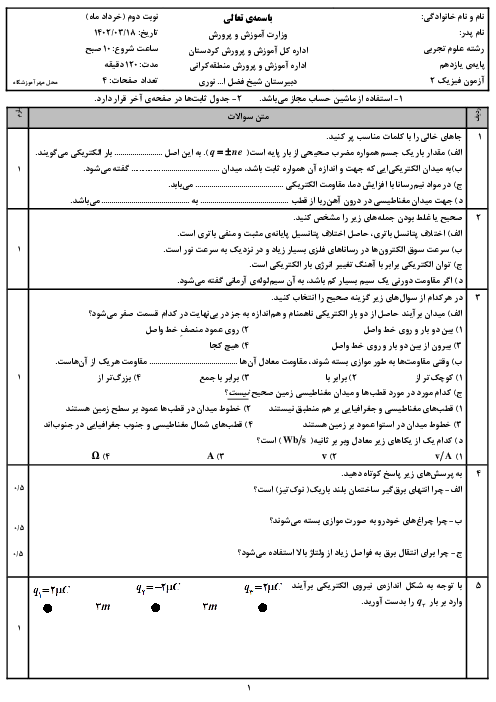
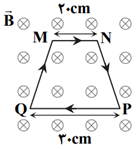
مطابق شكل، حلقۀ ذوزنقه‌ای شكل حامل جريان $I$، درون ميدان مغناطيسی يكنواختی قرار دارد. كدام رابطه بين نيروی مغناطيسی وارد بر اضلاع $MN$ و $PQ$ درست است؟
${{\overrightarrow{F}}_{MN}}=-\frac{2}{3}{{\overrightarrow{F}}_{PQ}}$
2 )
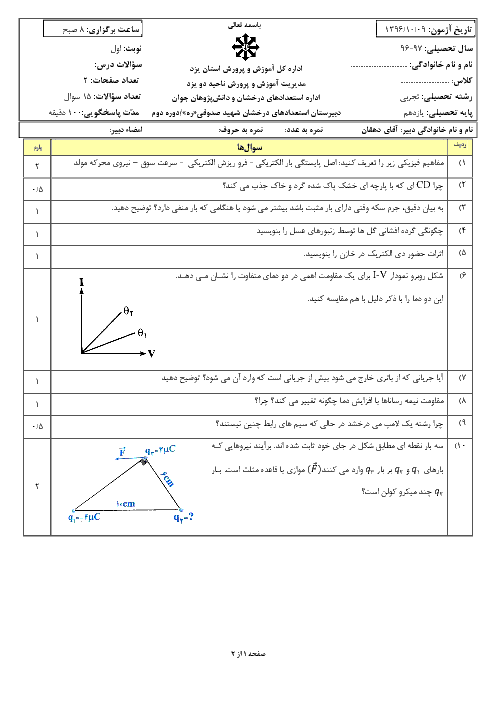
${{\overrightarrow{F}}_{MN}}=\frac{2}{3}{{\overrightarrow{F}}_{PQ}}$
3 )
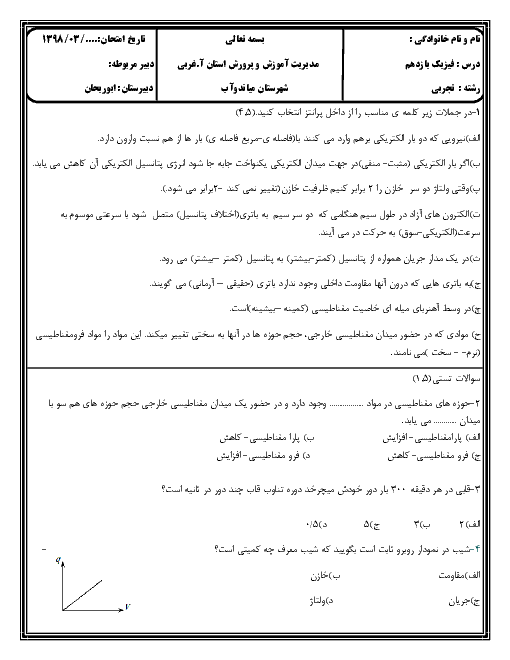
${{\overrightarrow{F}}_{MN}}=-\frac{3}{2}{{\overrightarrow{F}}_{PQ}}$
4 )
${{\overrightarrow{F}}_{MN}}=\frac{3}{2}{{\overrightarrow{F}}_{PQ}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
مجید میرزائی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...