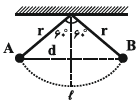
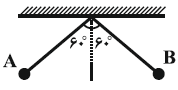
مطابق شكل زير آونگی از نقطه‌ی $A$ رها می‌شود و پس از مدت $2$ ثانيه برای اولين بار به نقطه‌ی $B$ در طرف مقابل میرسد. اگر اندازه‌ی سرعت متوسط گلوله‌ی آونگ $1/5\frac{m}{s}$ باشد، تندی متوسط گلوله چند متر بر ثانيه است؟
1 )
$\sqrt{3\pi }$
$\frac{\sqrt{3}}{3}\pi $
3 )
$\frac{\pi }{3}$
4 )
$\pi $
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...