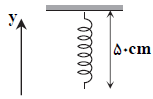
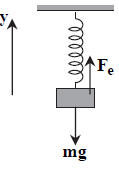
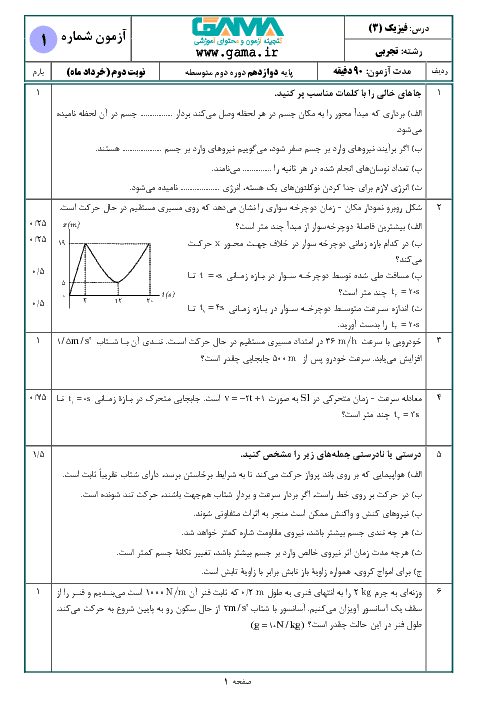
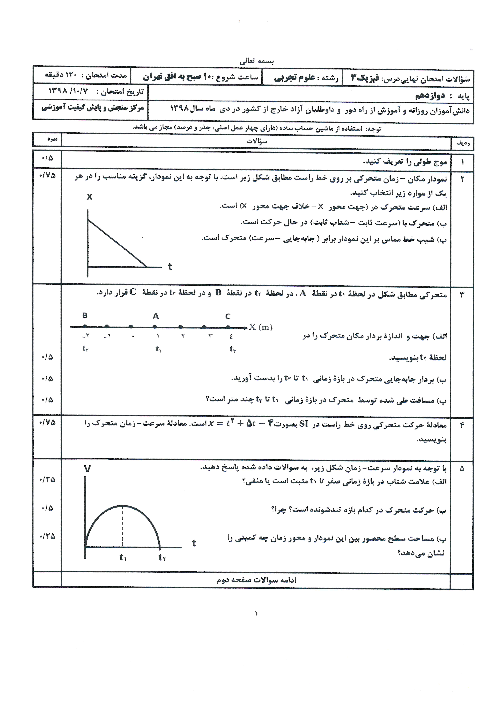
فنری با جرم ناچيز به طول $50cm$ و ثابت $200\frac{N}{m}$ مطابق شكل به سقف آويزان است. وزنهی $2kg$ را به انتهای فنر متصل و رها میكنيم تا به طرف پايين حركت نمايد. در لحظهای كه شتاب وزنه به $\overrightarrow{a}=(2\frac{m}{{{s}^{2}}})\overrightarrow{j}$ میرسد، طول فنر چند سانتیمتر است؟ $(g=10\frac{N}{kg})$