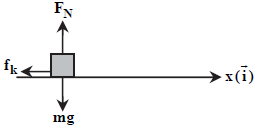
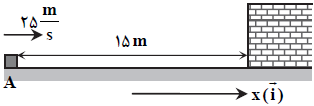
مطابق شكل، جسم كوچكی به جرم گرم را با تندی اوليه‌ی از نقطه‌ی روی یک سطح افقی دارای اصطکاک به‌سمت دیوار پرتاب می‌کنیم. اگر تندی جسم هنگام بازگشت و در لحظه‌ی جدا… | فیزیک (3) تجربی دوازدهم شماره 89100

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

قسمت 2: معرفی برخی از نیروهای خاص فیزیک (3) تجربی دوازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

مطابق شكل، جسم كوچكی به جرم $50$ گرم را با تندی اوليه‌ی $25\frac{m}{s}$ از نقطه‌ی $A$ روی یک سطح افقی دارای اصطکاک به‌سمت دیوار پرتاب می‌کنیم. اگر تندی جسم هنگام بازگشت و در لحظه‌ی جدا شدن از دیوار با تندی آن هنگام برخورد به دیوار برابر و مدت‌زمان برخورد جسم به دیوار $0/2$ ثانیه باشد، نیروی متوسطی که در این مدت از طرف دیوار به جسم وارد می‌شود، کدام است؟ $({{\mu }_{k}}=0/75\,,\,g=10\frac{m}{{{s}^{2}}})$

1 )

صفر

2 )

$(-20N)\overrightarrow{i}$

3 )

$(-10N)\overrightarrow{i}$

4 )

$(+10N)\overrightarrow{i}$

نمایش پاسخ

$-{{f}_{k}}=ma\Rightarrow -{{\mu }_{k}}{{F}_{N}}=ma\xrightarrow{{{F}_{N}}=mg}-{{\mu }_{k}}mg=ma\Rightarrow a=-{{\mu }_{k}}g=-0/75\times 10=-7/5\frac{m}{{{s}^{2}}}$

سرعت جسم در لحظه‌ی برخورد به دیوار برابر است با:

${{v}^{2}}-{{v}_{{}^\circ }}^{2}=2a\Delta x\Rightarrow {{v}^{2}}-625=2\times (-7/5)(15)\Rightarrow v=20\frac{m}{s}$

درهنگام جدا شدن جسم، سرعت جسم همان مقدار ولی در جهت مخالف است؛ یعنی سرعت جسم هنگام جدا شدن از دیوار $(-20\frac{m}{s})\overrightarrow{i}$ بوده و نیروی متوسط وارد بر جسم برابر است با:

$\overrightarrow{F}=m\overrightarrow{a}=m\frac{{{\overrightarrow{v}}_{2}}-{{\overrightarrow{v}}_{1}}}{\Delta t}=\frac{50}{1000}\times \frac{-20\overrightarrow{i}-20\overrightarrow{i}}{0/2}=-10\overrightarrow{i}(N)$