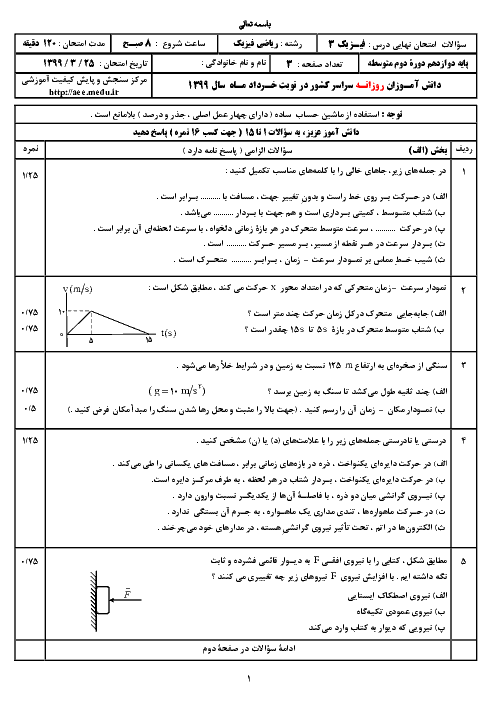
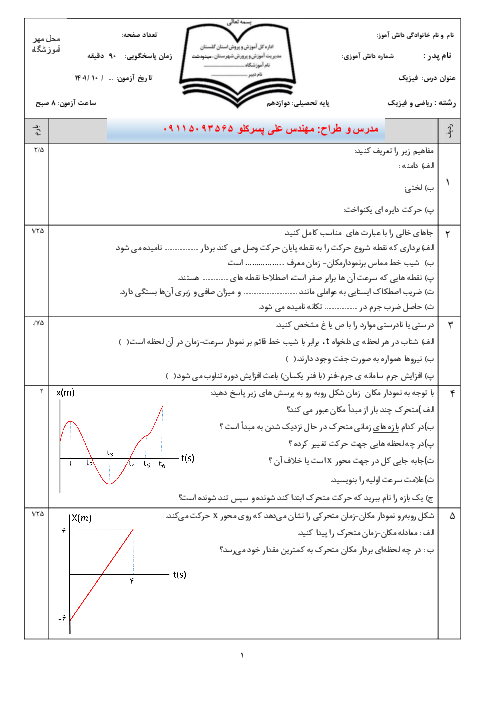
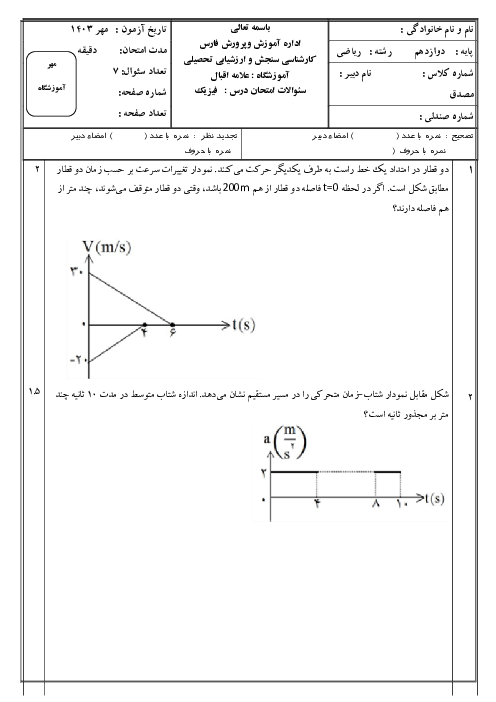
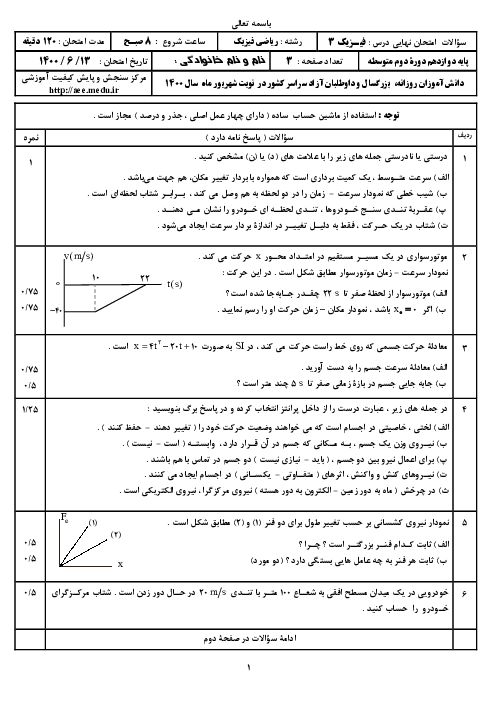
در يک حركت هماهنگ ساده، بيشينۀ اندازهٔ شتاب نوسانگر $۲۰{{\pi }^{۲}}\frac{m}{{{s}^{۲}}}$ و بيشينۀ تندی آن $\pi \frac{m}{s}$ است. اندازهٔ شتاب متوسط نوسانگر در مدتی كه بدون تغيير جهت از يک انتهای مسير تا مركز نوسان (وضع تعادل) حركت می‌كند، چند متر بر مربع ثانيه است؟