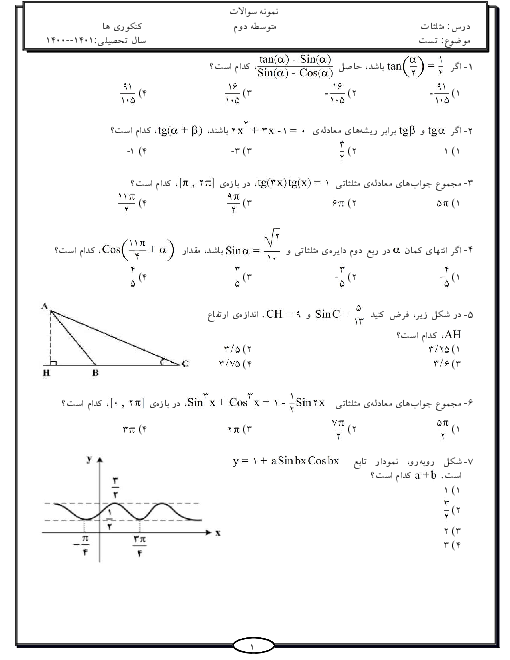
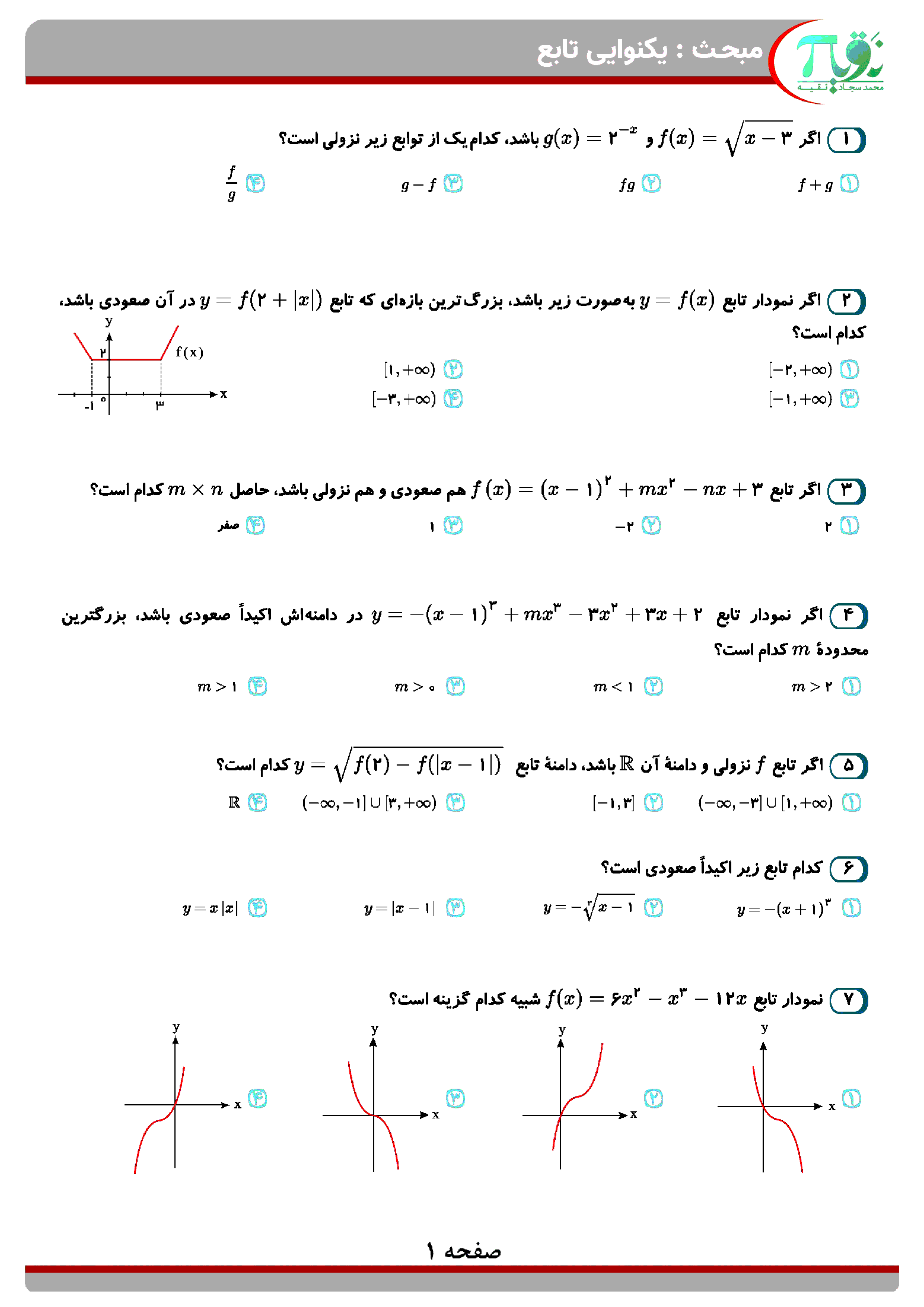
تابع f با ضابطهٔ $f(x) = \left\{ {\begin{array}{*{20}{c}} {2bx + c}&{x > a} \\ {3{x^2}}&{x \leqslant a} \end{array}} \right.$ روی $\mathbb{R}$ مشتقپذیر است. مقدار ${a^3} + b - c$ کدام است؟
${(a + 1)^3} - 1$
2 )
${(a + 1)^3} + 1$
3 )
${(a - 1)^3} - 1$
4 )
${(a - 1)^3} + 1$
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...