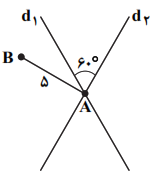
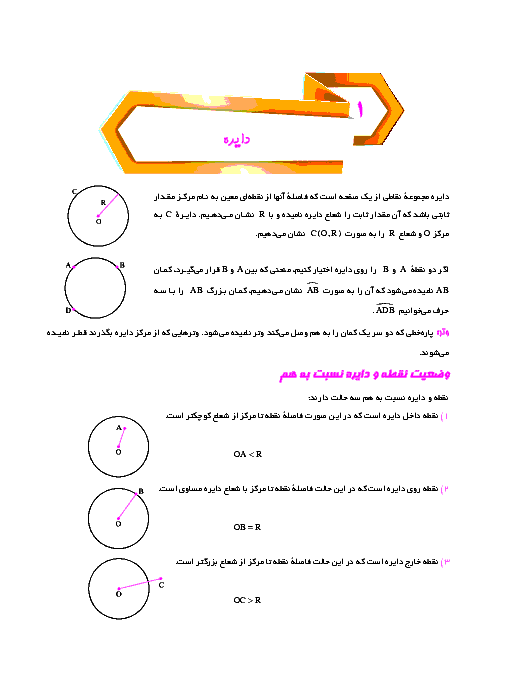
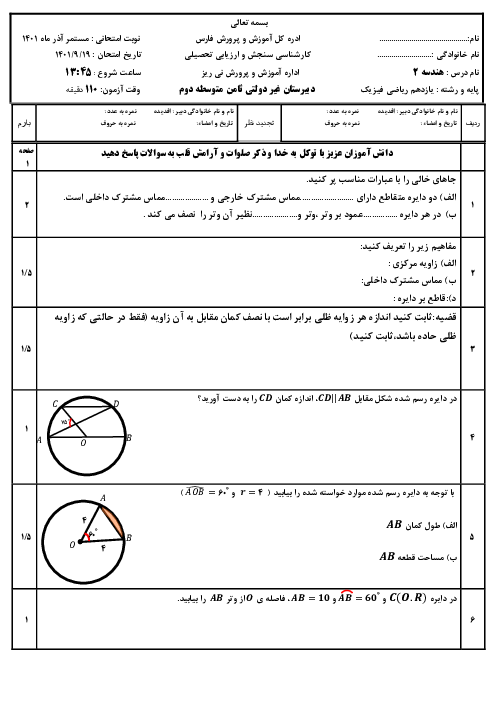
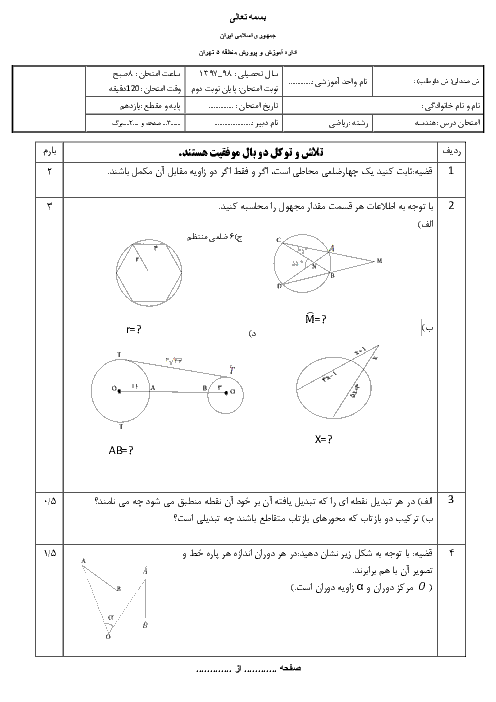
نكته‌ی 1: تركيب دو بازتاب محوری با محورهای متقاطع برابر است با يك دوران به مركز محل تقاطع دو خط و زاويه‌ی دو برابر زاويه‌ی بين دو خط.

نكته‌ی 2: بازتاب و دوران، طولپا هستند.

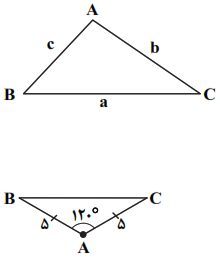
نكته‌ی 3: بر طبق قضيه‌ی سينوس‌ها در مثلث ABC با اضلاع a، b و c، داریم:

$\frac{a}{\operatorname{Sin}\hat{A}}=\frac{b}{\operatorname{Sin}\hat{B}}=\frac{c}{\operatorname{Sin}\hat{C}}=2R$

که در آن، R شعاع دایره‌ی محیطی مثلث ABC است.

با توجه به نکته‌ی 1، نقطه‌ی C از دوران نقطه‌ی B به مرکز A و زاویه‌ی ${{120}^{{}^\circ }}$ به‌دست می‌آید و از آن‌جایی‌که با توجه به نکته‌ی 2، دوران طولپاست، پس $AB=AC$ یعنی مثلث ABC مطابق شکل زیر با زاویه‌ی رأس ${{120}^{{}^\circ }}$، متساوی‌الساقین است و داریم:

$\hat{B}=\hat{C}=\frac{{{180}^{{}^\circ }}-{{120}^{{}^\circ }}}{2}={{30}^{{}^\circ }}$

و در نهایت با توجه به نکته‌ی 3،‌خواهیم داشت:

$\frac{AB}{\operatorname{Sin}\hat{C}}=2R\Rightarrow \frac{5}{\operatorname{Sin}{{30}^{{}^\circ }}}=2R\Rightarrow R=\frac{5}{2\times \frac{1}{2}}=5$